User Guide to machine-check
Formal verification of digital systems made easierPreface
This is the user guide for machine-check, a tool/library for formal verification of arbitrary digital systems described in the Rust programming language using finite-state machines.
Unlike testing, which determines if a specification holds for a small set of system executions, formal verification can determine whether it holds for all possible executions. While only tiny systems can be verified by brute force, machine-check uses an intelligent approach to make verification of larger and more capable systems possible.
Unlike some other verifiers, machine-check is designed to be sound, never returning a wrong verification result1, and complete, theoretically always returning a result in finite time and memory. While arbitrary finite-systems can be represented, the current focus is on verification of systems comprised of machine-code programs executed on embedded processors.
Interested? Read the Quickstart.
ℹ️ Machine-check version 0.7.0 has been released on 29th October 2025, with support for more expressive properties and other improvements. Read the accompanying blogpost.
🛠️ Currently, machine-check is in active development. While the basic building blocks are in place, some details may still change considerably in the future.
Useful links
- The main website
- The blog
- Latest stable version at crates.io
- Latest stable API documentation at docs.rs
- Development repository at GitHub
Just like machine-check, this book is available under the Apache 2.0 or MIT licence. Its original sources are available at GitHub.
-
In other words, if the wrong verification result is returned, this is always considered a bug in machine-check. If you encounter a bug, please report it. ↩
Quickstart
If you are a Rust user, you can skip to the usage. You can also try out the quick example from the machine-check readme.
Setting up Rust
Machine-check is a tool for verification of systems written in a subset of the Rust programming language. In the context of Rust, it works as a library you use in your code. If you do not use Rust yet, you need to install Rust and learn its basics first. Fortunately, describing finite-state machines does not use that many Rust concepts, so you can just skim over the first few chapters (although preferably 10) of the Rust Book, try out a few examples, and return to the book if you do not understand something.
To start using machine-check, create a new binary Rust package using Rust's package manager cargo:
$ cargo new hello-machine-check
Creating binary (application) `hello-machine-check` package
note: see more `Cargo.toml` keys and their definitions at https://doc.rust-lang.org/cargo/reference/manifest.html
In the created hello-machine-check directory, there is a package config file Cargo.toml and a hello-world placeholder in src/main.rs:
fn main() {
println!("Hello, world!");
}
You can run the program using cargo run in the hello-machine-check directory:
$ cargo run
Compiling hello-machine-check v0.1.0 (<your path>\hello-machine-check)
Finished `dev` profile [unoptimized + debuginfo] target(s) in 1.07s
Running `target\debug\hello-machine-check.exe`
Hello, world!
Let us now move to actually using machine-check.
Using machine-check
In your Cargo.toml, add the following dependency:
[dependencies]
machine-check = "0.7.0"
You can start using machine-check in Rust now. Let's create a minimal somewhat interesting system to verify. Put this in your src/main.rs:
#[machine_check::machine_description] mod machine_module { use ::machine_check::Bitvector; use ::std::{ clone::Clone, cmp::{Eq, PartialEq}, fmt::Debug, hash::Hash, }; #[derive(Clone, PartialEq, Eq, Hash, Debug)] pub struct Input { increment_value: Bitvector<1>, } #[derive(Clone, PartialEq, Eq, Hash, Debug)] pub struct Param {} #[derive(Clone, PartialEq, Eq, Hash, Debug)] pub struct State { value: Bitvector<4>, } #[derive(Clone, PartialEq, Eq, Hash, Debug)] pub struct System {} impl ::machine_check::Machine for System { type Input = Input; type Param = Param; type State = State; fn init(&self, _input: &Input, _param: &Param) -> State { State { value: Bitvector::<4>::new(0), } } fn next(&self, state: &State, input: &Input, _param: &Param) -> State { let mut next_value = state.value; if input.increment_value == Bitvector::<1>::new(1) { next_value = next_value + Bitvector::<4>::new(1); } State { value: next_value } } } } fn main() { let system = machine_module::System {}; machine_check::run(system); }
That is a lot of code. Fortunately, most of it is just boilerplate around the contents of the Input and State structures and init and next functions which define a Finite State Machine. We will discuss how the machine is described later; for now, just know that the state contains a four-bit field value that is initially zero and after that, each next step of the machine is determined by looking at a single-bit input field increment_value, incrementing value if increment_value is 1 and leaving value as-is otherwise. Ready for some verification?
Verifying
Machine-check can verify properties in propositional μ-calculus. For simplicity, we will discuss verifying Computation Tree Logic (CTL) properties in the main part of the book and discuss the μ-calculus in an advanced chapter. For example, using a CTL property, we can determine that from every reachable state of the system, we can, through some sequence of inputs, get to a state where value is zero:
$ cargo run -- --property 'AG![EF![value == 0]]'
Compiling hello-machine-check v0.1.0 ((...)\hello-machine-check)
Finished `dev` profile [unoptimized + debuginfo] target(s) in 11.98s
warning: the following packages contain code that will be rejected by a future version of Rust: partitions v0.2.4
note: to see what the problems were, use the option `--future-incompat-report`, or run `cargo report future-incompatibilities --id 2`
Running `target\debug\hello-machine-check.exe --property "AG![EF![value == 0]]"`
[2025-10-28T22:19:37Z INFO machine_check] Starting verification.
[2025-10-28T22:19:37Z INFO machine_check::verify] Verifying the inherent property first.
[2025-10-28T22:19:37Z INFO machine_check::verify] The inherent property holds, proceeding to the given property.
[2025-10-28T22:19:37Z INFO machine_check::verify] Verifying the given property.
[2025-10-28T22:19:37Z INFO machine_check] Verification ended.
+-------------------------------+
| Result: HOLDS |
+-------------------------------+
| Refinements: 16 |
| Generated states: 48 |
| Final states: 16 |
| Generated transitions: 64 |
| Final transitions: 33 |
+-------------------------------+
Machine-check was able to quickly verify that the supplied property holds.
🛠️ You can safely ignore the warning about the package
partitions, which is currently internally used by machine-check. This warning should be rectified in the next release.
While the example system under verification is very simple, machine-check integrates advanced techniques that make verification of more complex systems possible, such as ones combining a processor and a machine-code program. In the following chapters, we will discuss the properties that can be verified, the system descriptions, the Command-line Interface, and the Graphical User Interface that can be used to understand the results of verification or the reasons for the inability to feasibly verify a property against a system.
Properties
Machine-check can verify properties in Computation Tree Logic and propositional μ-calculus. Since the μ-calculus is not easy to understand, we will discuss the properties in Computation Tree Logic first and discuss the μ-calculus later in an advanced chapter.
Let's start with a very simple property: is the value zero at the start of the computation?
$ cargo run -- --property 'value == 0'
Finished `dev` profile [unoptimized + debuginfo] target(s) in 0.13s
warning: the following packages contain code that will be rejected by a future version of Rust: partitions v0.2.4
note: to see what the problems were, use the option `--future-incompat-report`, or run `cargo report future-incompatibilities --id 2`
Running `target\debug\hello-machine-check.exe --property "value == 0"`
[2025-10-28T22:20:12Z INFO machine_check] Starting verification.
[2025-10-28T22:20:12Z INFO machine_check::verify] Verifying the inherent property first.
[2025-10-28T22:20:12Z INFO machine_check::verify] The inherent property holds, proceeding to the given property.
[2025-10-28T22:20:12Z INFO machine_check::verify] Verifying the given property.
[2025-10-28T22:20:12Z INFO machine_check] Verification ended.
+------------------------------+
| Result: HOLDS |
+------------------------------+
| Refinements: 0 |
| Generated states: 6 |
| Final states: 5 |
| Generated transitions: 6 |
| Final transitions: 6 |
+------------------------------+
Let's not focus on what the messages or numbers mean and just look at the verification result. Machine-check has determined that the property value == 0 holds, which matches the definition of the init function.
⚠️ Currently, if the system has multiple initial states, machine-check follows the convention that the property holds exactly if it holds in all of the initial states.
This behaviour may change in the future once system parametrisation is implemented.
Verifying a single state is admittedly quite boring. The real power of the Computation Tree Logic (CTL) is that we can reason about things temporally, looking into states in the future. For example, we can use the temporal operator AX[φ] which means "for all paths, φ will hold in the next state" to say "for all paths, value will be 0 in the current state". In machine-check, since the paths are determined only by the machine inputs, we can also say "for all input sequences" instead of "for all paths", which can be more intutive. In machine-check property syntax, we write this as AX![value == 0]. The exclamation mark after AX: this is done as the property syntax emulates Rust syntax and it makes a lot of sense to think of the temporal properties as macros, since they change what the variables inside them represent. That aside, let's try to verify.
💡️ In some shells such as
bash, the exclamation mark (!) can have a special meaning even when double-quoted. Always put the properties in single quotes when supplying them on command line shell to prevent problems.
$ cargo run -- --property 'AX![value == 0]'
Finished `dev` profile [unoptimized + debuginfo] target(s) in 0.10s
warning: the following packages contain code that will be rejected by a future version of Rust: partitions v0.2.4
note: to see what the problems were, use the option `--future-incompat-report`, or run `cargo report future-incompatibilities --id 2`
Running `target\debug\hello-machine-check.exe --property "AX![value == 0]"`
[2025-10-28T22:20:32Z INFO machine_check] Starting verification.
[2025-10-28T22:20:32Z INFO machine_check::verify] Verifying the inherent property first.
[2025-10-28T22:20:32Z INFO machine_check::verify] The inherent property holds, proceeding to the given property.
[2025-10-28T22:20:32Z INFO machine_check::verify] Verifying the given property.
[2025-10-28T22:20:32Z INFO machine_check] Verification ended.
+------------------------------+
| Result: DOES NOT HOLD |
+------------------------------+
| Refinements: 1 |
| Generated states: 8 |
| Final states: 5 |
| Generated transitions: 9 |
| Final transitions: 7 |
+------------------------------+
💡️ In this handbook, the verifier executable is built in debug mode, and uses the default strategy, using
cargo run -- --property <PROPERTY>.If verification becomes too slow for your system, try compiling in release mode:
cargo run --release -- --property <PROPERTY>This will slow down compilation but produce a more optimised executable that will be able to verify faster. You can also try to use machine-check with the decay strategy (this can make verification faster or slower based on the system):
cargo run --release -- --property <PROPERTY> --strategy decayNote that the
--argument that separates the arguments for the build tool cargo from the arguments that will be passed to the built program and processed by machine-check.
Of course this does not hold: we can increment the value, so value will no longer be zero in all of the next states! But what about it being zero in at least one next state? That should hold: if the increment_value input is 0, we will retain zero value. Instead of AX[φ], we will use the EX[φ] operator: there exists a path where φ holds in next state. Let's try to verify.
$ cargo run -- --property 'EX![value == 0]'
Finished `dev` profile [unoptimized + debuginfo] target(s) in 0.10s
warning: the following packages contain code that will be rejected by a future version of Rust: partitions v0.2.4
note: to see what the problems were, use the option `--future-incompat-report`, or run `cargo report future-incompatibilities --id 2`
Running `target\debug\hello-machine-check.exe --property "EX![value == 0]"`
[2025-10-28T22:20:44Z INFO machine_check] Starting verification.
[2025-10-28T22:20:44Z INFO machine_check::verify] Verifying the inherent property first.
[2025-10-28T22:20:44Z INFO machine_check::verify] The inherent property holds, proceeding to the given property.
[2025-10-28T22:20:44Z INFO machine_check::verify] Verifying the given property.
[2025-10-28T22:20:44Z INFO machine_check] Verification ended.
+------------------------------+
| Result: HOLDS |
+------------------------------+
| Refinements: 1 |
| Generated states: 8 |
| Final states: 5 |
| Generated transitions: 9 |
| Final transitions: 7 |
+------------------------------+
Wonderful. But we have just started to discover the possibilities. While AX and EX can be used to reason about the states directly after the current one, CTL also contains operators we can use to reason about unbounded periods of time. AG[φ] means that for all input sequences, the property φ will hold globally, i.e. in all time instants including and after this one. In our example, for all input sequences, value will globally be lesser or equal to 15. (In case AG is used as the outer operator, this is usually written as "in all reachable states, value will be lesser or equal to 15.") Writing this as a machine-check property, we have to explicitly say that value should be compared as an unsigned number using as_unsigned before comparing it:
$ cargo run -- --property 'AG![as_unsigned(value) <= 15]'
Finished `dev` profile [unoptimized + debuginfo] target(s) in 0.10s
warning: the following packages contain code that will be rejected by a future version of Rust: partitions v0.2.4
note: to see what the problems were, use the option `--future-incompat-report`, or run `cargo report future-incompatibilities --id 2`
Running `target\debug\hello-machine-check.exe --property "AG![as_unsigned(value) <= 15]"`
[2025-10-28T22:21:05Z INFO machine_check] Starting verification.
[2025-10-28T22:21:05Z INFO machine_check::verify] Verifying the inherent property first.
[2025-10-28T22:21:05Z INFO machine_check::verify] The inherent property holds, proceeding to the given property.
[2025-10-28T22:21:05Z INFO machine_check::verify] Verifying the given property.
[2025-10-28T22:21:05Z INFO machine_check] Verification ended.
+------------------------------+
| Result: HOLDS |
+------------------------------+
| Refinements: 0 |
| Generated states: 6 |
| Final states: 5 |
| Generated transitions: 6 |
| Final transitions: 6 |
+------------------------------+
While this would not hold for a constant lesser than 15 (you can try it), EG[φ] means that there is an infinite input sequence where φ holds globally. Reasonably, we can expect that value stays to be zero when the increment_value input is always kept 0:
$ cargo run -- --property 'EG![value == 0]'
Finished `dev` profile [unoptimized + debuginfo] target(s) in 0.11s
warning: the following packages contain code that will be rejected by a future version of Rust: partitions v0.2.4
note: to see what the problems were, use the option `--future-incompat-report`, or run `cargo report future-incompatibilities --id 2`
Running `target\debug\hello-machine-check.exe --property "EG![value == 0]"`
[2025-10-28T22:21:13Z INFO machine_check] Starting verification.
[2025-10-28T22:21:13Z INFO machine_check::verify] Verifying the inherent property first.
[2025-10-28T22:21:13Z INFO machine_check::verify] The inherent property holds, proceeding to the given property.
[2025-10-28T22:21:13Z INFO machine_check::verify] Verifying the given property.
[2025-10-28T22:21:13Z INFO machine_check] Verification ended.
+------------------------------+
| Result: HOLDS |
+------------------------------+
| Refinements: 1 |
| Generated states: 8 |
| Final states: 5 |
| Generated transitions: 9 |
| Final transitions: 7 |
+------------------------------+
Great. What if we try to verify if it stays to be 3?
$ cargo run -- --property 'EG![value == 3]'
Finished `dev` profile [unoptimized + debuginfo] target(s) in 0.10s
warning: the following packages contain code that will be rejected by a future version of Rust: partitions v0.2.4
note: to see what the problems were, use the option `--future-incompat-report`, or run `cargo report future-incompatibilities --id 2`
Running `target\debug\hello-machine-check.exe --property "EG![value == 3]"`
[2025-10-28T22:21:26Z INFO machine_check] Starting verification.
[2025-10-28T22:21:26Z INFO machine_check::verify] Verifying the inherent property first.
[2025-10-28T22:21:26Z INFO machine_check::verify] The inherent property holds, proceeding to the given property.
[2025-10-28T22:21:26Z INFO machine_check::verify] Verifying the given property.
[2025-10-28T22:21:26Z INFO machine_check] Verification ended.
+------------------------------+
| Result: DOES NOT HOLD |
+------------------------------+
| Refinements: 0 |
| Generated states: 6 |
| Final states: 5 |
| Generated transitions: 6 |
| Final transitions: 6 |
+------------------------------+
It does not, since value is 0 at the start. To reason about the future, we can use the AF and EF operators. AF[φ] means that for all input sequences, φ holds eventually. This can be either currently or in the future. EF[φ] means that there exists an input sequence for which φ holds eventually, which is a bit more interesting in the context of our example:
$ cargo run -- --property 'EF![as_unsigned(value) == 3]'
Finished `dev` profile [unoptimized + debuginfo] target(s) in 0.14s
warning: the following packages contain code that will be rejected by a future version of Rust: partitions v0.2.4
note: to see what the problems were, use the option `--future-incompat-report`, or run `cargo report future-incompatibilities --id 2`
Running `target\debug\hello-machine-check.exe --property "EF![as_unsigned(value) == 3]"`
[2025-10-28T22:21:34Z INFO machine_check] Starting verification.
[2025-10-28T22:21:34Z INFO machine_check::verify] Verifying the inherent property first.
[2025-10-28T22:21:34Z INFO machine_check::verify] The inherent property holds, proceeding to the given property.
[2025-10-28T22:21:34Z INFO machine_check::verify] Verifying the given property.
[2025-10-28T22:21:34Z INFO machine_check] Verification ended.
+-------------------------------+
| Result: HOLDS |
+-------------------------------+
| Refinements: 3 |
| Generated states: 13 |
| Final states: 6 |
| Generated transitions: 16 |
| Final transitions: 10 |
+-------------------------------+
The nice thing about CTL is that we can build more interesting reasoning from nesting the operators. Let us suppose we want to make sure that there exists an input sequence which eventually reaches a state where there exists an input sequence where value is then globally equal to 3:
$ cargo run -- --property 'EF![EG![value == 3]]'
Finished `dev` profile [unoptimized + debuginfo] target(s) in 0.10s
warning: the following packages contain code that will be rejected by a future version of Rust: partitions v0.2.4
note: to see what the problems were, use the option `--future-incompat-report`, or run `cargo report future-incompatibilities --id 2`
Running `target\debug\hello-machine-check.exe --property "EF![EG![value == 3]]"`
[2025-10-28T22:21:42Z INFO machine_check] Starting verification.
[2025-10-28T22:21:42Z INFO machine_check::verify] Verifying the inherent property first.
[2025-10-28T22:21:42Z INFO machine_check::verify] The inherent property holds, proceeding to the given property.
[2025-10-28T22:21:42Z INFO machine_check::verify] Verifying the given property.
[2025-10-28T22:21:42Z INFO machine_check] Verification ended.
+-------------------------------+
| Result: HOLDS |
+-------------------------------+
| Refinements: 4 |
| Generated states: 17 |
| Final states: 8 |
| Generated transitions: 21 |
| Final transitions: 13 |
+-------------------------------+
For even more descriptive properties, we can use the AU, EU, AR, and ER CTL operators1. These take two arguments. Nothwithstanding the difference in the input sequence requirements, A[φ]U[ψ] and E[φ]U[ψ] stipulate that φ should hold until ψ holds, although not necessarily in the position where ψ first holds, and ψ must hold eventually. A[φ]R[ψ] and E[φ]R[ψ] stipulate that φ releases ψ: ψ has to hold before and including the point where φ first holds, and if φ never holds, ψ must hold globally. Notice how AU/EU and AR/ER are essentially extensions of AF/EF and AG/EG, respectively.
In machine-check properties, we write these operators as macros with two arguments. For example, we can make sure that there exists an input sequence where value is lesser than 3 until it is 3 (which occurs eventually):
$ cargo run -- --property 'EU![as_unsigned(value) < 3, value == 3]'
Finished `dev` profile [unoptimized + debuginfo] target(s) in 0.10s
warning: the following packages contain code that will be rejected by a future version of Rust: partitions v0.2.4
note: to see what the problems were, use the option `--future-incompat-report`, or run `cargo report future-incompatibilities --id 2`
Running `target\debug\hello-machine-check.exe --property "EU![as_unsigned(value) < 3, value == 3]"`
[2025-10-28T22:22:04Z INFO machine_check] Starting verification.
[2025-10-28T22:22:04Z INFO machine_check::verify] Verifying the inherent property first.
[2025-10-28T22:22:04Z INFO machine_check::verify] The inherent property holds, proceeding to the given property.
[2025-10-28T22:22:04Z INFO machine_check::verify] Verifying the given property.
[2025-10-28T22:22:04Z INFO machine_check] Verification ended.
+-------------------------------+
| Result: HOLDS |
+-------------------------------+
| Refinements: 3 |
| Generated states: 13 |
| Final states: 6 |
| Generated transitions: 16 |
| Final transitions: 10 |
+-------------------------------+
And for all input sequences, value being 3 releases the requirement for value to be at most 3:
$ cargo run -- --property 'AR![value == 3, as_unsigned(value) <= 3]'
Finished `dev` profile [unoptimized + debuginfo] target(s) in 0.10s
warning: the following packages contain code that will be rejected by a future version of Rust: partitions v0.2.4
note: to see what the problems were, use the option `--future-incompat-report`, or run `cargo report future-incompatibilities --id 2`
Running `target\debug\hello-machine-check.exe --property "AR![value == 3, as_unsigned(value) <= 3]"`
[2025-10-28T22:22:15Z INFO machine_check] Starting verification.
[2025-10-28T22:22:15Z INFO machine_check::verify] Verifying the inherent property first.
[2025-10-28T22:22:15Z INFO machine_check::verify] The inherent property holds, proceeding to the given property.
[2025-10-28T22:22:15Z INFO machine_check::verify] Verifying the given property.
[2025-10-28T22:22:15Z INFO machine_check] Verification ended.
+-------------------------------+
| Result: HOLDS |
+-------------------------------+
| Refinements: 3 |
| Generated states: 13 |
| Final states: 6 |
| Generated transitions: 16 |
| Final transitions: 10 |
+-------------------------------+
Note the differences in the formulation of the previous two properties.
In addition to CTL operators, machine-check properties support logical not (!), and (&&), or (||) operators, letting us construct more descriptive properties. For example, we can say that in all reachable states, value being 5 implies that, for all input sequences, it will be 5 or 6 in the next step. Since an implication φ ⇒ ψ can be written as ¬φ ∨ ψ, we can verify:
$ cargo run -- --property 'AG![!(value == 5) || AX![value == 5 || value == 6]]'
Finished `dev` profile [unoptimized + debuginfo] target(s) in 0.10s
warning: the following packages contain code that will be rejected by a future version of Rust: partitions v0.2.4
note: to see what the problems were, use the option `--future-incompat-report`, or run `cargo report future-incompatibilities --id 2`
Running `target\debug\hello-machine-check.exe --property "AG![!(value == 5) || AX![value == 5 || value == 6]]"`
[2025-10-28T22:22:23Z INFO machine_check] Starting verification.
[2025-10-28T22:22:23Z INFO machine_check::verify] Verifying the inherent property first.
[2025-10-28T22:22:23Z INFO machine_check::verify] The inherent property holds, proceeding to the given property.
[2025-10-28T22:22:23Z INFO machine_check::verify] Verifying the given property.
[2025-10-28T22:22:23Z INFO machine_check] Verification ended.
+-------------------------------+
| Result: HOLDS |
+-------------------------------+
| Refinements: 16 |
| Generated states: 48 |
| Final states: 16 |
| Generated transitions: 64 |
| Final transitions: 33 |
+-------------------------------+
Last but not least, we can verify a recovery property stating that in all reachable states, there exists an input sequence where we can get back to value being zero:
$ cargo run -- --property 'AG![EF![value == 0]]'
Finished `dev` profile [unoptimized + debuginfo] target(s) in 0.10s
warning: the following packages contain code that will be rejected by a future version of Rust: partitions v0.2.4
note: to see what the problems were, use the option `--future-incompat-report`, or run `cargo report future-incompatibilities --id 2`
Running `target\debug\hello-machine-check.exe --property "AG![EF![value == 0]]"`
[2025-10-28T22:22:31Z INFO machine_check] Starting verification.
[2025-10-28T22:22:31Z INFO machine_check::verify] Verifying the inherent property first.
[2025-10-28T22:22:31Z INFO machine_check::verify] The inherent property holds, proceeding to the given property.
[2025-10-28T22:22:31Z INFO machine_check::verify] Verifying the given property.
[2025-10-28T22:22:31Z INFO machine_check] Verification ended.
+-------------------------------+
| Result: HOLDS |
+-------------------------------+
| Refinements: 16 |
| Generated states: 48 |
| Final states: 16 |
| Generated transitions: 64 |
| Final transitions: 33 |
+-------------------------------+
Notably, this property is not possible to verify using formal verification tools that use verification based on the traditional Counterexample-based Abstraction Refinement. Machine-check can verify this property thanks to the used Three-valued Abstraction Refinement framework.
-
The AR and ER operators are usually not described in the literature on CTL, but can be derived from other operators. ↩
Property Format
The properties of machine-check are described in a subset of Rust expressions, augmented with temporal logic operators and some syntax sugar for easily expressing values.
Available Variables
All fields of the struct State of the machine under verification are available to use just using their struct field names. Together, these variables represent the current state. The fields must be of machine-check types Unsigned and Signed, Bitvector, or BitvectorArray.
🛠️ Currently, the signedness of bit-vectors in the system is not known by the property, i.e. Unsigned and Signed fields of
Stateare seen by the property as Bitvector variables.
Standard Expressions and Syntax Sugar
Standard Rust operators that are supported by the types of fields are also available in property expressions. This notably includes BitvectorArray read (array_field[bitvector_index]) and short-circuiting AND (&&) and OR (||) for Booleans obtained from equality, comparison, or temporal logic operators.
Also supported are constructor functions for the types. The functions must be used by their full paths. For example, ::machine_check::Unsigned::<8>::new(0) != ::machine_check::Unsigned::<8>::new(1) is a valid type. Of course, this is a bit unwieldy, so literals in equalities/comparisons are coerced to the appropriate machine-check type if it is possible to infer that, e.g. value == 0 is a valid property expression if value is a bitvector field.
Also supported are the functions as_signed and as_unsigned, demonstrated previously. Note that the syntax sugar for literal coercion and as_signed/as_unsigned are specific to properties only and cannot be used when writing systems.
Temporal Logic Operators
The temporal logic operators are written as Rust macros. There are two basic types of them: Computation Tree Logic operators and μ-calculus fixed-point operators. Generally, they expect property expressions given as their arguments to evaluate to Boolean values, and they return a Boolean value. The argument expressions are essentially evaluated in new contexts, using the field values of the state they operate on instead of the outer values.
The CTL operators EX!, AX!, EF!, AF!, EG! and AG! take a single property expression. The CTL operators EU!, AU!, ER!, and AR! take two property expressions, in the order of arguments usual for CTL. The μ-calculus fixed-point operators described in an advanced chapter take two arguments, where the first one is an identifier of a new fixed-point variable that can be used within any nesting of the temporal operators (unless shadowed) and the second one is the property expression to evaluate.
Systems
To explain the form of the systems in machine-check, let us return to the Quickstart example:
#[machine_check::machine_description] mod machine_module { use ::machine_check::Bitvector; use ::std::{ clone::Clone, cmp::{Eq, PartialEq}, fmt::Debug, hash::Hash, }; #[derive(Clone, PartialEq, Eq, Hash, Debug)] pub struct Input { increment_value: Bitvector<1>, } #[derive(Clone, PartialEq, Eq, Hash, Debug)] pub struct Param {} #[derive(Clone, PartialEq, Eq, Hash, Debug)] pub struct State { value: Bitvector<4>, } #[derive(Clone, PartialEq, Eq, Hash, Debug)] pub struct System {} impl ::machine_check::Machine for System { type Input = Input; type Param = Param; type State = State; fn init(&self, _input: &Input, _param: &Param) -> State { State { value: Bitvector::<4>::new(0), } } fn next(&self, state: &State, input: &Input, _param: &Param) -> State { let mut next_value = state.value; if input.increment_value == Bitvector::<1>::new(1) { next_value = next_value + Bitvector::<4>::new(1); } State { value: next_value } } } } fn main() { let system = machine_module::System {}; machine_check::run(system); }
That is a lot of code. Fortunately, most of it just boils to the Input, Param, and State structures, and init and next functions which define a Finite State Machine. Let us unpack it bit by bit. Do not worry if you do not understand everything.
To enable formal verification of properties of digital systems using more intelligent means than brute-force computation, machine-check transforms them in a Rust macro which is called by placing an attribute #[machine_check::machine_description] on an inner module, in this case called machine_module. The code that goes through the macro is enriched with verification analogues for fast verification. As the macro only supports a small subset of Rust code, it will produce a (hopefully useful) error if it does not understand something. However, you can still write any Rust code you want outside the module.
Since the machine_description macro cannot read the outside of the module, it does not assume anything about it, such as that the identifier Clone refers to the trait::std::clone::Clone which is usually imported in the Rust prelude: you might have changed Clone to mean something else outside. As such, you need to import it in the module using the absolute path ::std::clone::Clone. As referring to ::std::clone::Clone each time it is used is annoying, we bring it in scope with a use declaration, so we can just write Clone again and machine_description knows it really is ::std::clone::Clone.
Onto the more interesting part, the structure input:
#![allow(unused)] fn main() { #[derive(Clone, PartialEq, Eq, Hash, Debug)] pub struct Input { increment_value: Bitvector<1>, } }
This defines how the input of the Finite-State Machine (FSM) looks like. Do not worry about the derive line; this is needed simply to ensure that it is sensible to manipulate using machine-check. We define a structure Input that has exactly one field increment_value of type Bitvector<1>. Bitvector is a type provided by machine-check that has no signedness information and wrapping arithmetic operations. The number in angled brackets determines the bit-width, i.e. increment-value has only a single bit. So, basically, the input of the FSM is just a single bit. The next lines are:
#![allow(unused)] fn main() { #[derive(Clone, PartialEq, Eq, Hash, Debug)] pub struct Param {} }
This defines the parameters of the system, which syntactically behave similarly to the inputs but have a special meaning for verification. For simplicity, we will not use parameters in this chapter, and describe them in a later chapter. This means we just leave the Param structure empty to get a non-parametric system.
The state structure is more interesting:
#![allow(unused)] fn main() { #[derive(Clone, PartialEq, Eq, Hash, Debug)] pub struct State { value: Bitvector<4>, } impl ::machine_check::State for State {} }
There is just one field value in the state, a four bits wide bit-vector. What's next?
#![allow(unused)] fn main() { #[derive(Clone, PartialEq, Eq, Hash, Debug)] pub struct System {} impl ::machine_check::Machine for System { type Input = Input; type Param = Param; type State = State; fn init(&self, _input: &Input, _param: &Param) -> State { State { value: Bitvector::<4>::new(0), } } fn next(&self, state: &State, input: &Input, _param: &Param) -> State { let mut next_value = state.value; if input.increment_value == Bitvector::<1>::new(1) { next_value = next_value + Bitvector::<4>::new(1); } State { value: next_value, } } } }
This is where the fun begins. We define a structure System that has no fields and implement a trait ::machine_check::Machine on it that will determine the actual FSM.
#![allow(unused)] fn main() { type Input = Input; type Param = Param; type State = State; }
The type declarations say that the input type of the FSM (left-side Input) is the structure Input we defined previously. Similarly, the FSM parameter type is the structure Param and the state type is the structure State. To describe the FSM, we also need is a function that creates the initial states of the FSM and a function that transforms a state to a next state, and this is exactly what we have.
#![allow(unused)] fn main() { fn init(&self, _input: &Input, _param: &Param) -> State { State { value: Bitvector::<4>::new(0), } } }
The init function takes the system structure (which has no fields in our case, so is quite useless in this situation), the input, and the parameter, creating an initial machine state based on that. Our init function just creates a state where value is a four-bit bit-vector with the value zero.
🛠️ Currently, the initialisation function also takes the input structure as an argument, possibly creating multiple initial states. This will most likely change in the future when parametric systems are implemented.
The state function is a bit more interesting:
#![allow(unused)] fn main() { fn next(&self, state: &State, input: &Input, _param: &Param) -> State { let mut next_value = state.value; if input.increment_value == Bitvector::<1>::new(1) { next_value = next_value + Bitvector::<4>::new(1); } State { value: next_value, } } }
We create a mutable variable next_value based on the value of the current state, and if the input field increment_value is equal to one, we add 1 to the value. Note that despite the Bitvector not having any signedness, addition is the same for unsigned and signed numbers in wrap-around arithmetic, so we can do this nicely here. We then return the next value.
So, we have defined a machine that contains a four-bit bit-vector value that is incremented in each step if increment_value is one, otherwise, it is left as-is.
Instances and Panics
It is useful to be able to change the behaviour of the system under verification at runtime, e.g. using command-line arguments, so that the system does not need to be changed and recompiled to change some part of its behaviour. Consider the part of the example from the previous section:
(...) #[derive(Clone, PartialEq, Eq, Hash, Debug)] pub struct System {} impl ::machine_check::Machine for System { type Input = Input; type Param = Param; type State = State; fn init(&self, _input: &Input, _param: &Param) -> State { State { value: Bitvector::<4>::new(0), } } fn next(&self, state: &State, input: &Input, _param: &Param) -> State { let mut next_value = state.value; if input.increment_value == Bitvector::<1>::new(1) { next_value = next_value + Bitvector::<4>::new(1); } State { value: next_value, } } } (...) fn main() { let system = machine_module::System {}; machine_check::run(system); }
Let us suppose that we want to specify the maximum value, after which it wraps, and supply the value from the main function. We can do this by extending the struct System with a new field as follows:
(...) use ::machine_check::Unsigned; use ::std::convert::Into; #[derive(Clone, PartialEq, Eq, Hash, Debug)] pub struct System { pub max_value: Bitvector<4>, } impl ::machine_check::Machine for System { type Input = Input; type Param = Param; type State = State; fn init(&self, _input: &Input, _param: &Param) -> State { State { value: Bitvector::<4>::new(0), } } fn next(&self, state: &State, input: &Input, _param: &Param) -> State { let mut next_value = state.value; if input.increment_value == Bitvector::<1>::new(1) { next_value = next_value + Bitvector::<4>::new(1); } if Into::<Unsigned<4>>::into(next_value) > Into::<Unsigned<4>>::into(self.max_value) { next_value = Bitvector::<4>::new(0); } State { value: next_value } } } (...) fn main() { print!("Write the maximum system value: "); std::io::Write::flush(&mut std::io::stdout()).expect("Should flush standard output"); let mut read_string = String::new(); std::io::stdin() .read_line(&mut read_string) .expect("Should read string from standard input"); let read_max_value: u64 = read_string .trim() .parse() .expect("Input should be an unsigned integer"); let system = machine_module::System { max_value: machine_check::Bitvector::new(read_max_value), }; machine_check::run(system); }
We introduced a new four-bit bit-vector field max_value in the System struct, and added a condition in the next function that converts the next value and maximum value to an unsigned interpretation, and if the next value is larger, it is zeroed. In the main function, we print the command to the user to write the maximum system value, and after we read it, we construct the system accordingly. The main function is fully standard Rust. We can now try to verify that there exists an input sequence using which we eventually get to value being 10, using a few different values:
$ cargo run -- --property 'EF![value == 10]'
Compiling hello-machine-check v0.1.0 ((...)\hello-machine-check)
Finished `dev` profile [unoptimized + debuginfo] target(s) in 2.02s
warning: the following packages contain code that will be rejected by a future version of Rust: partitions v0.2.4
note: to see what the problems were, use the option `--future-incompat-report`, or run `cargo report future-incompatibilities --id 2`
Running `target\debug\hello-machine-check.exe --property "EF![value == 10]"`
Write the maximum system value: 5
[2025-10-28T22:23:19Z INFO machine_check] Starting verification.
[2025-10-28T22:23:19Z INFO machine_check::verify] Verifying the inherent property first.
[2025-10-28T22:23:19Z INFO machine_check::verify] The inherent property holds, proceeding to the given property.
[2025-10-28T22:23:19Z INFO machine_check::verify] Verifying the given property.
[2025-10-28T22:23:19Z INFO machine_check] Verification ended.
+-------------------------------+
| Result: DOES NOT HOLD |
+-------------------------------+
| Refinements: 6 |
| Generated states: 19 |
| Final states: 6 |
| Generated transitions: 25 |
| Final transitions: 13 |
+-------------------------------+
$ cargo run -- --property 'EF![value == 10]'
Finished `dev` profile [unoptimized + debuginfo] target(s) in 0.12s
warning: the following packages contain code that will be rejected by a future version of Rust: partitions v0.2.4
note: to see what the problems were, use the option `--future-incompat-report`, or run `cargo report future-incompatibilities --id 2`
Running `target\debug\hello-machine-check.exe --property "EF![value == 10]"`
Write the maximum system value: 12
[2025-10-28T22:23:36Z INFO machine_check] Starting verification.
[2025-10-28T22:23:36Z INFO machine_check::verify] Verifying the inherent property first.
[2025-10-28T22:23:36Z INFO machine_check::verify] The inherent property holds, proceeding to the given property.
[2025-10-28T22:23:36Z INFO machine_check::verify] Verifying the given property.
[2025-10-28T22:23:36Z INFO machine_check] Verification ended.
+-------------------------------+
| Result: HOLDS |
+-------------------------------+
| Refinements: 10 |
| Generated states: 33 |
| Final states: 13 |
| Generated transitions: 43 |
| Final transitions: 24 |
+-------------------------------+
$ cargo run -- --property 'EF![value == 10]'
Finished `dev` profile [unoptimized + debuginfo] target(s) in 0.10s
warning: the following packages contain code that will be rejected by a future version of Rust: partitions v0.2.4
note: to see what the problems were, use the option `--future-incompat-report`, or run `cargo report future-incompatibilities --id 2`
Running `target\debug\hello-machine-check.exe --property "EF![value == 10]"`
Write the maximum system value: 20
thread 'main' panicked at (...)\mck-0.7.0\src\bitvector\concr\support.rs:18:25:
Bitvector (width 4) value 20 is outside bounds [0,15]
note: run with `RUST_BACKTRACE=1` environment variable to display a backtrace
error: process didn't exit successfully: `target\debug\hello-machine-check.exe --property "EF![value == 10]"` (exit code: 101)
For the values of 5 and 12, everything works as intended. Since the four-bit bit-vector cannot be constructed by Bitvector::new with the value 20, the program panics.
🛠️ It is possible to use command-line arguments for the construction of systems, although the current form is highly unstable.
See the source code of machine-check-avr for details.
Panics and the Inherent Property
Sometimes, we want to disallow verification of a system containing some instance data. For example, we are implementing a processor and did not describe some instruction yet, or the instruction is disallowed by the processor specification itself. We can use the Rust macros panic!, todo!, and unimplemented! to preclude verification of properties in some cases. For example, suppose that we did not have the time to describe the behaviour of max_value within the introduced condition, so we wrote:
if Into::<Unsigned<4>>::into(next_value) > Into::<Unsigned<4>>::into(self.max_value) {
::std::todo!("Zero the next value when it is greater than max value");
}
Now, the verification will return an error when verifying a property and a panic can eventually occur with some input sequence (i.e. EF[panic]):
$ cargo run -- --property 'EF![value == 10]'
Compiling hello-machine-check v0.1.0 ((...)\hello-machine-check)
Finished `dev` profile [unoptimized + debuginfo] target(s) in 1.39s
warning: the following packages contain code that will be rejected by a future version of Rust: partitions v0.2.4
note: to see what the problems were, use the option `--future-incompat-report`, or run `cargo report future-incompatibilities --id 2`
Running `target\debug\hello-machine-check.exe --property "EF![value == 10]"`
Write the maximum system value: 5
[2025-10-28T22:24:37Z INFO machine_check] Starting verification.
[2025-10-28T22:24:37Z INFO machine_check::verify] Verifying the inherent property first.
[2025-10-28T22:24:37Z ERROR machine_check] Verification returned an error.
+----------------------------------------------------------------------------------------------------------+
| Result: ERROR ("inherent panic") |
+----------------------------------------------------------------------------------------------------------+
| Refinements: 6 |
| Generated states: 22 |
| Final states: 9 |
| Generated transitions: 28 |
| Final transitions: 16 |
| Inherent panic message: "not yet implemented: Zero the next value when it is greater than max value" |
+----------------------------------------------------------------------------------------------------------+
However, in case the panic cannot occur, the verification will proceed normally:
$ cargo run -- --property 'EF![value == 15]'
Finished `dev` profile [unoptimized + debuginfo] target(s) in 0.10s
warning: the following packages contain code that will be rejected by a future version of Rust: partitions v0.2.4
note: to see what the problems were, use the option `--future-incompat-report`, or run `cargo report future-incompatibilities --id 2`
Running `target\debug\hello-machine-check.exe --property "EF![value == 15]"`
Write the maximum system value: 15
[2025-10-28T22:24:52Z INFO machine_check] Starting verification.
[2025-10-28T22:24:52Z INFO machine_check::verify] Verifying the inherent property first.
[2025-10-28T22:24:52Z INFO machine_check::verify] The inherent property holds, proceeding to the given property.
[2025-10-28T22:24:52Z INFO machine_check::verify] Verifying the given property.
[2025-10-28T22:24:52Z INFO machine_check] Verification ended.
+-------------------------------+
| Result: HOLDS |
+-------------------------------+
| Refinements: 15 |
| Generated states: 47 |
| Final states: 17 |
| Generated transitions: 62 |
| Final transitions: 33 |
+-------------------------------+
This is the meaning of the messages when verifying: first, the inherent property (no panics can be reached) is verified, then, the given property (EF![value == 15] in our case) is verified. We can also verify just the inherent property itself:
$ cargo run -- --inherent
Finished `dev` profile [unoptimized + debuginfo] target(s) in 0.09s
warning: the following packages contain code that will be rejected by a future version of Rust: partitions v0.2.4
note: to see what the problems were, use the option `--future-incompat-report`, or run `cargo report future-incompatibilities --id 2`
Running `target\debug\hello-machine-check.exe --inherent`
Write the maximum system value: 10
[2025-10-28T22:25:11Z INFO machine_check] Starting verification.
[2025-10-28T22:25:11Z INFO machine_check::verify] Verifying the inherent property.
[2025-10-28T22:25:11Z INFO machine_check] Verification ended.
+----------------------------------------------------------------------------------------------------------+
| Result: DOES NOT HOLD |
+----------------------------------------------------------------------------------------------------------+
| Refinements: 11 |
| Generated states: 36 |
| Final states: 14 |
| Generated transitions: 47 |
| Final transitions: 26 |
| Inherent panic message: "not yet implemented: Zero the next value when it is greater than max value" |
+----------------------------------------------------------------------------------------------------------+
$ cargo run -- --inherent
Finished `dev` profile [unoptimized + debuginfo] target(s) in 0.10s
warning: the following packages contain code that will be rejected by a future version of Rust: partitions v0.2.4
note: to see what the problems were, use the option `--future-incompat-report`, or run `cargo report future-incompatibilities --id 2`
Running `target\debug\hello-machine-check.exe --inherent`
Write the maximum system value: 15
[2025-10-28T22:25:24Z INFO machine_check] Starting verification.
[2025-10-28T22:25:24Z INFO machine_check::verify] Verifying the inherent property.
[2025-10-28T22:25:24Z INFO machine_check] Verification ended.
+------------------------------+
| Result: HOLDS |
+------------------------------+
| Refinements: 0 |
| Generated states: 6 |
| Final states: 5 |
| Generated transitions: 6 |
| Final transitions: 6 |
+------------------------------+
It is also possible to assume the inherent property holds by using the --assume-inherent command-line argument. In this case, if the inherent property actually does not hold, any verification results obtained while assuming it will be meaningless.
System Format
The systems are written in a subset of Rust. Generally, the machine_description macro will emit the code that was written enriched by internal modules and implementations, so if the original code is not compilable by Rust without errors, it will not become compilable. Machine-check will also emit errors if it cannot translate the system code to the verification equivalents.
The systems generally should conform to the structure presented previously. The examples and the source code of the machine-check-avr description can be used for inspiration. As such, only the general principles of defining the structures and writing the functions to achieve the desired system behaviour will be detailed here.
🛠️ The system format and accepted Rust constructs may change in the future so that the descriptions can be written more easily.
Structures and Fields
Structures can be defined as follows:
#![allow(unused)] fn main() { #[derive(Clone, PartialEq, Eq, Hash, Debug)] pub struct ExampleStruct { pub bitvector_field: ::machine_check::Bitvector<4>, pub unsigned_field: ::machine_check::Unsigned<13>, pub signed_field: ::machine_check::Signed<32>, pub bitvector_array_field: ::machine_check::BitvectorArray<14, 12>, } }
The currently supported types are all provided by machine-check. There are three bit-vector types Bitvector, Unsigned, and Signed for variables that contain a binary value with the width determined by the generic constant W, with 2ʷ values possible. All of the types offer wrapping arithmetic, and they differ in the interpretation of the contained value. In Unsigned, the values are considered to be unsigned, and in Signed, they are considered signed in two's complement. This determines the behaviour of width extension, right shift and comparison operations. In Bitvector, these operations are not provided, although the type still is weakly unsigned when being constructed via new and used to index arrays. The Bitvector type is useful when constructing systems such as processor-based systems, where the memory cells do not necessarily have any signedness information, and the signedness is provided by the instruction currently operating on the cells. This can greatly reduce description errors in selecting the wrong operation signedness.
The bit-vector types can be converted into each other by using the standard library Into. In addition to supporting standard operators (excluding division, remainder, and operator-assignment), they also support width extension or narrowing via the Ext trait. The Signed type is currently not possible to construct via new like the other bit-vector types.
The type BitvectorArray is a power-of-2 bit-vector array where the first generic constant determines the index width (its power of two gives the array length) and the second one determines the element width. This makes it possible to ensure there are no possible panics when indexing. The array is retained using a sparse representation, ensuring that it is possible to construct e.g. a 48-bit-length array filled with zeros in constant time before assigning the values just to the cells of interest.
Functions
The current expressivity in functions is fairly restricted. In addition to the init and next functions that are implemented for the trait ::machine_check::Machine, it is also possible to write functions in the inherent implementation of the struct:
#![allow(unused)] fn main() { impl System { fn my_func() -> Bitvector<4> { Bitvector::<4>::new(3) } } }
All functions must have a return type that is one of the types known by machine-check (the basic provided types or defined structs) and can take an arbitrary numbers of parameters that are either of these types or are immutable references to them. This can be used for composition of complex behaviours, such as in the machine-check-avr description
As for the statements inside the functions, please consult the examples and the machine-check-avr description to build an intuition on what is supported. Notably, the type inference is currently much weaker than that of Rust, so explicit type declarations might be necessary to get rid of failed type inference errors from machine-check. It is currently not possible to use method calls, so e.g. converting to an four-bit unsigned type must be performed as:
#![allow(unused)] fn main() { ::std::convert::Into::<Unsigned<4>>::into(variable) }
Similarly, bit extension or narrowing to eight bits (which must be done on Unsigned or Signed so the signedness is known) must be performed as:
#![allow(unused)] fn main() { ::machine_check::Ext::<8>::ext(variable) }
In addition to panic macros discussed previously, the bitmask_switch macro can be used for easier implementation of e.g. processor instructions. Examples of it can be found in simple_risc and the machine-check-avr description.
In case machine-check gives cryptic errors when the description is being compiled, you can try to return the description to the previous state where it compiled and carefully change things to pinpoint what breaks the translation, or comment out the machine_description macro temporarily to see if the code is invalid Rust, as the Rust compiler usually gives more understandable error messages.
Command-line Interface
In the previous chapters, the Command-Line Interface was used for controlling machine-check. When machine_check::run is called, it parses the program arguments and executes the verification accordingly. It is also possible to augment the arguments using machine_check::parse_args and machine_check::execute, although the actual way this works may change.
The full list of arguments can be found here or be printed using --help. The usually useful arguments are:
--inherent: Orders machine-check to verify the inherent property.--property <PROPERTY>: Orders machine-check to verify the given property. The inherent property is verified beforehand by default.--assume-inherent: Does not verify the inherent property before the given property. If the inherent property does not hold, the result of verifying the given property will be meaningless.--strategy <STRATEGY>: The strategy machine-check should take to verify the property. The choice of the strategy can have a drastic impact on verification time and memory used. There are currently three strategies:naive: Essentially constructs the state space of the system by brute force. Useless for most non-trivial systems as the state space is too big to use this strategy.default: Uses Three-valued Abstraction Refinement with input precision only. This is the default as it is a reasonable choice for many systems.decay: Uses a more aggressive abstraction and refinement approach with decay of computed states using step precision. This can verify some systems more easily than the default strategy, and is recommended if the default strategy does not produce a result in reasonable time.
The command-line interface is currently completely automatic: it starts verifying and returns the result once it is done (which, in many cases, may be after an infeasibly long time). Some progress information can be shown using the -v / --verbose flag (usable multiple times for more verbosity), but that is intended more as a debug tool and may slow down verification considerably, especially if the output is not rerouted to a file.
For a better insight into the workings of machine-check, use the Graphical User Interface.
Graphical User Interface
The machine-check GUI can be used to discover why the verification is taking too long or why the result does not match the expectations. As the GUI needs additional dependencies not available for all platforms and slows down compilation from scratch, it is disabled by default and must be enabled as a feature. Some dependencies may also need to be installed based on the operating system used.
Preparing for the Graphical User Interface
As the GUI uses the wry and tao libraries for rendering that are a part of the Tauri project, to be able to compile your crate with the machine-check GUI feature enabled, follow the prerequisites for your operating system (Linux, macOS, or Windows). On up-to-date Windows 10 and 11 specifically, no additional dependencies are needed. For Linux and macOS, some tools and libraries might be needed so that the build does not fail.
Add the following to your Cargo.toml:
[features]
gui = ["machine-check/gui"]
You can now compile and run your system description crate with the GUI enabled, which would be done like this:
$ cargo run --features gui -- --gui
The GUI will open prepared to verify the inherent property. You can also use --property to give a property for verification when the GUI opens.
Visualising the Quickstart Example
Continuing with hello-machine-check from Quickstart:
$ cargo run --features gui -- --property 'AG![EF![value == 0]]' --gui
(... compiling, building ~300 crates ...)
Compiling hello-machine-check v0.1.0 ((...)\hello-machine-check)
Finished `dev` profile [unoptimized + debuginfo] target(s) in 37.49s
warning: the following packages contain code that will be rejected by a future version of Rust: partitions v0.2.4
note: to see what the problems were, use the option `--future-incompat-report`, or run `cargo report future-incompatibilities --id 2`
Running `target\debug\hello-machine-check.exe --gui`
[2025-10-28T22:47:36Z INFO machine_check_gui::backend::window] GUI window opened
A window like this should open:
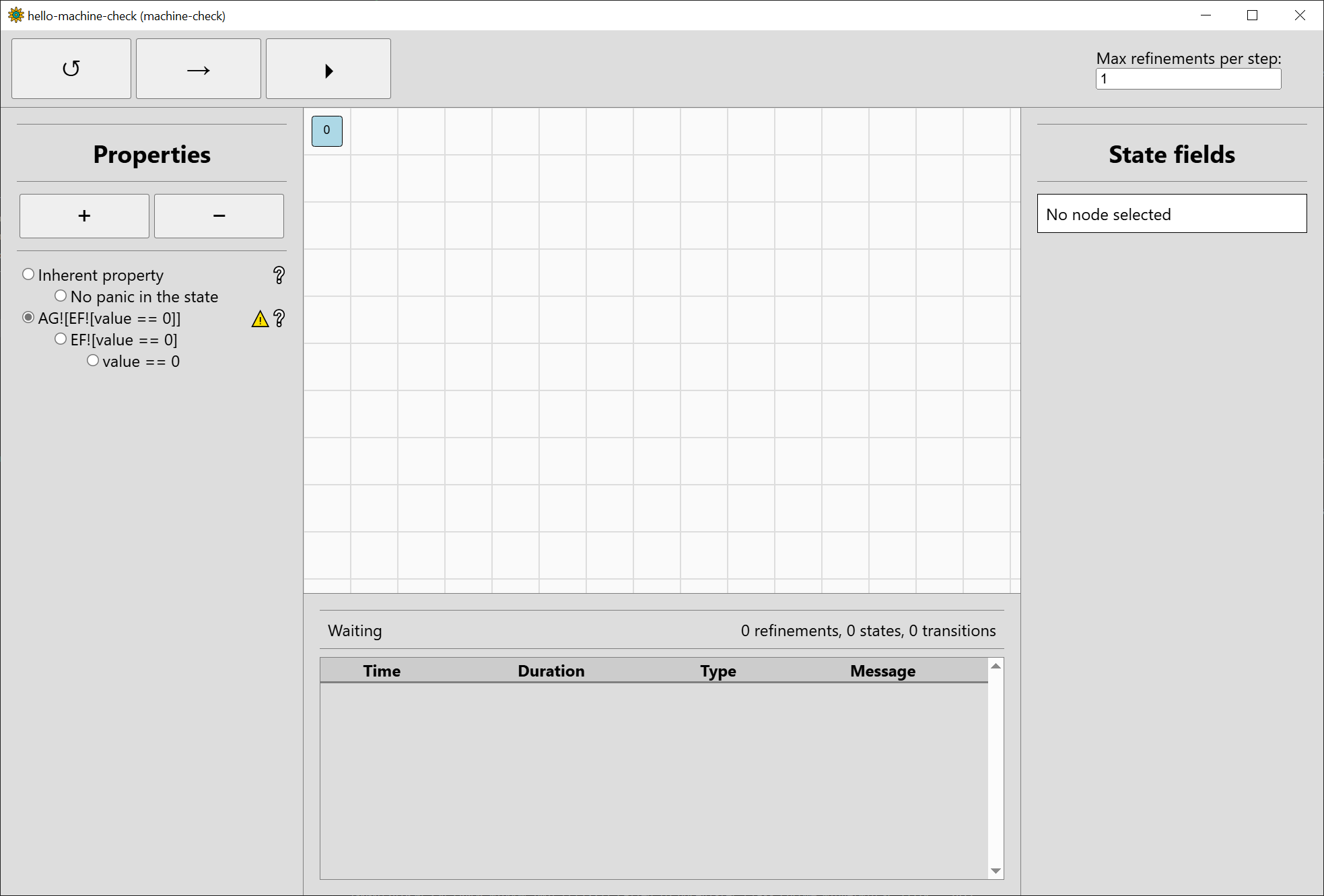
The interface is split to five main areas:
- The main state space visualisation area in the middle. In the above image, only the root node1 0 is shown as verification did not start yet.
- The top bar which controls verification, with three buttons to reset (↺), step (→), and run (⏵). The number of refinements to perform in each step can be controlled on the right side.
- The left bar which manages the properties considered and shows their current verification results.
The inherent property is always shown first. As we also gave the property
AG![EF![value == 0]], it is also shown. - The bottom bar which shows the current verification backend status (Waiting) and the number of refinements performed and states and transitions in the state space. Below that is a log of completed actions.
- The right bar which shows the values of the fields of the selected state. Currently, no state is selected.
So that we can discuss the progress of verification itself, click the step button (→) once. You can also use keyboard navigation (Tab, Shift-Tab, Enter) since the GUI is rendered as an HTML document. Five new states will be shown, click on the state with identifier 1 (#1 for short). If the main area is focused, you can also use your keyboard (the Home key selects the root node and arrows can be used to go between successive graph nodes or siblings). Right-clicking or middle-clicking the mouse allows you to drag the view of the main area.
The window should now look somewhat like this:
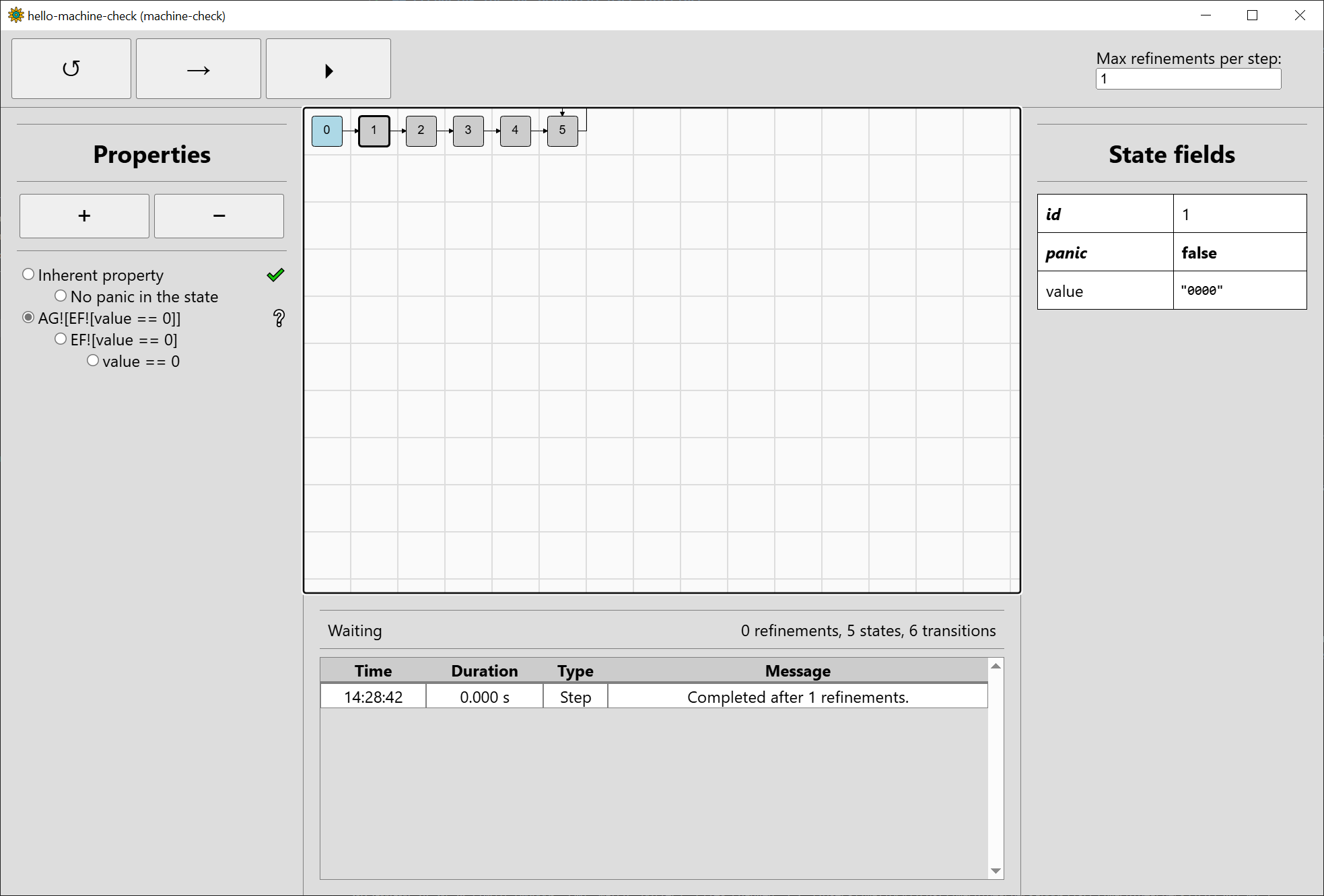
Recalling that our system from Quickstart had a single field value that was initialised to zero, we can see that #1 really
has value initialised to zero (displayed as "0000" in binary representation). There is no panic in this state, which is expected, since the example
features no panics whatsoever.
The state after #1 should be incremented based on the the input increment_value. But there is only one successor, state #2. We can navigate to it
to see that it has the value "000X". This is three-valued bit-vector abstraction: the abstract state #2 can stand for either "0000" or "0001". In
machine-check, it stands for at least one of them but not necessarily both. Moving to the next states, we can see that value changes to "00XX",
"0XXX", and lastly "XXXX" in #5, which just loops on itself. The behaviour is regular: when incrementing e.g. 00XX, it could stand for 0011, so we would
end up with 0100 after incrementing. However, it could also stand e.g. for 0010, so we would end up with 0011 after incrementing. To ensure that the
verification is sound (never returns a wrong result), machine-check ensures the resulting state "0XXX" subsumes all of the possibilities. As it uses
a special algorithm for this, the computation is faster than enumerating all the possibilities.
Even though the value is ultimately "XXXX", no panic occurs when going from any state to the next one. Therefore, as seen in the left properties bar, the
inherent property holds. The warning sign previously seen to the right of the recovery property also disappeared: it informed us that as the inherent
property had not yet been verified, the result of verifying the recovery property may be ultimately meaningless. (If you are unsure what a property
verification icon to the right of the property means, you can read the title text after hovering over it with mouse.)
While the inherent property has been verified, the visualised state space is now too abstract to verify the property AG![EF![value == 0]]. As such,
machine-check will perform a refinement of the abstract state space, regenerate its affected parts, and verify again. Step the verification again:
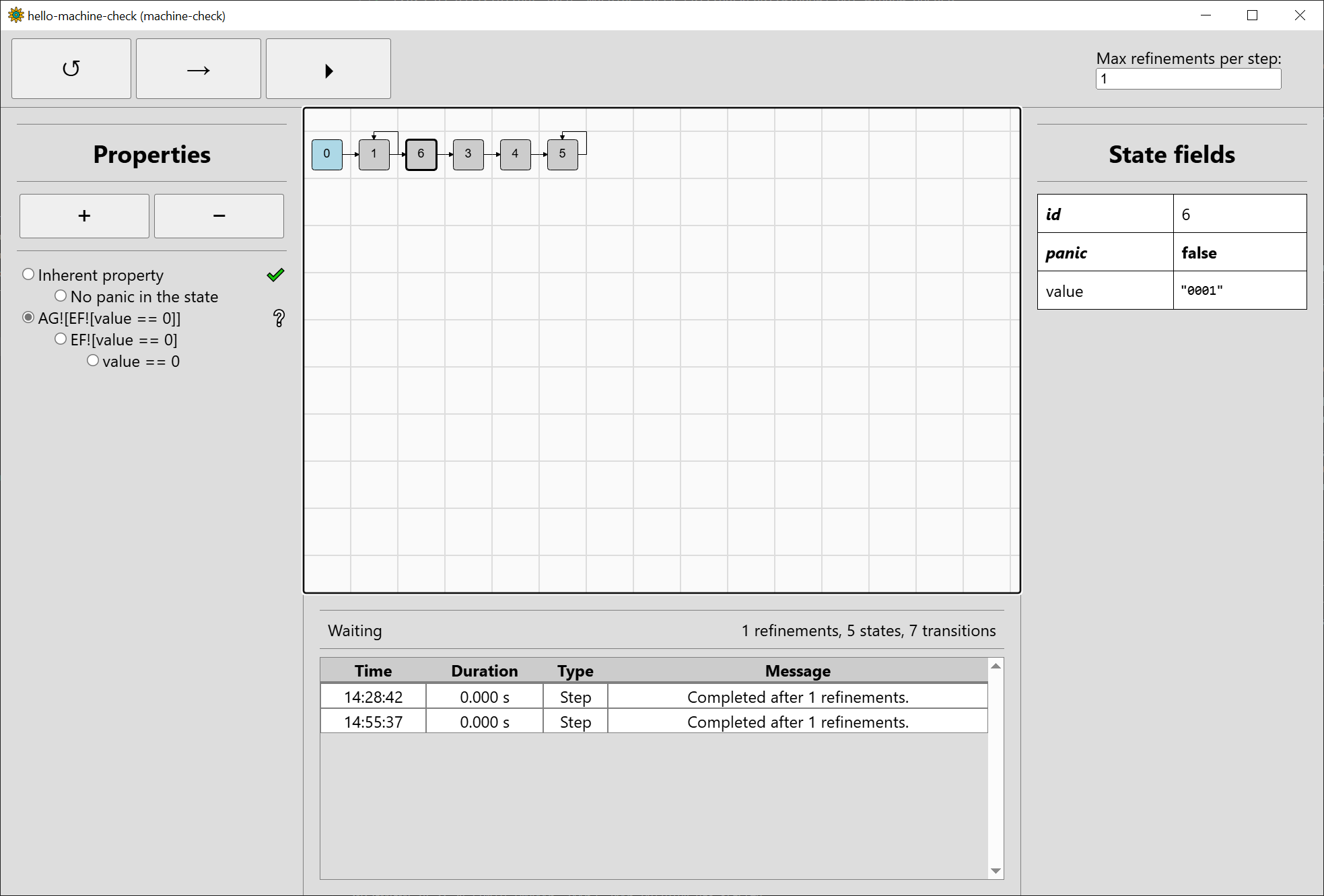
Machine-check decided to refine the input going from #1 to #2. This added a loop from #1 to itself (when increment_input is 0) and generated a new state #6
that, upon inspection, has value equal to "0001" (when increment_input is 1). Unfortunately, potentially incrementing "0001" again goes to "00XX" represented
by #3, so we have not really progressed much.
Let's now talk more about the property bar. Step the verification four more times. While the property AG![EF![value == 0]] is still unknown (symbolised by
the question mark to the right of the property), a nice aspect of Computation Tree Logic is that
we can compute whether the property holds or not from any state (i.e. considering the state is the sole initial state from which the property is computed),
and the temporal operators just combine this information from sub-properties. As such, we can visualise in which states each sub-property holds. Switch to
the sub-property value == 0:
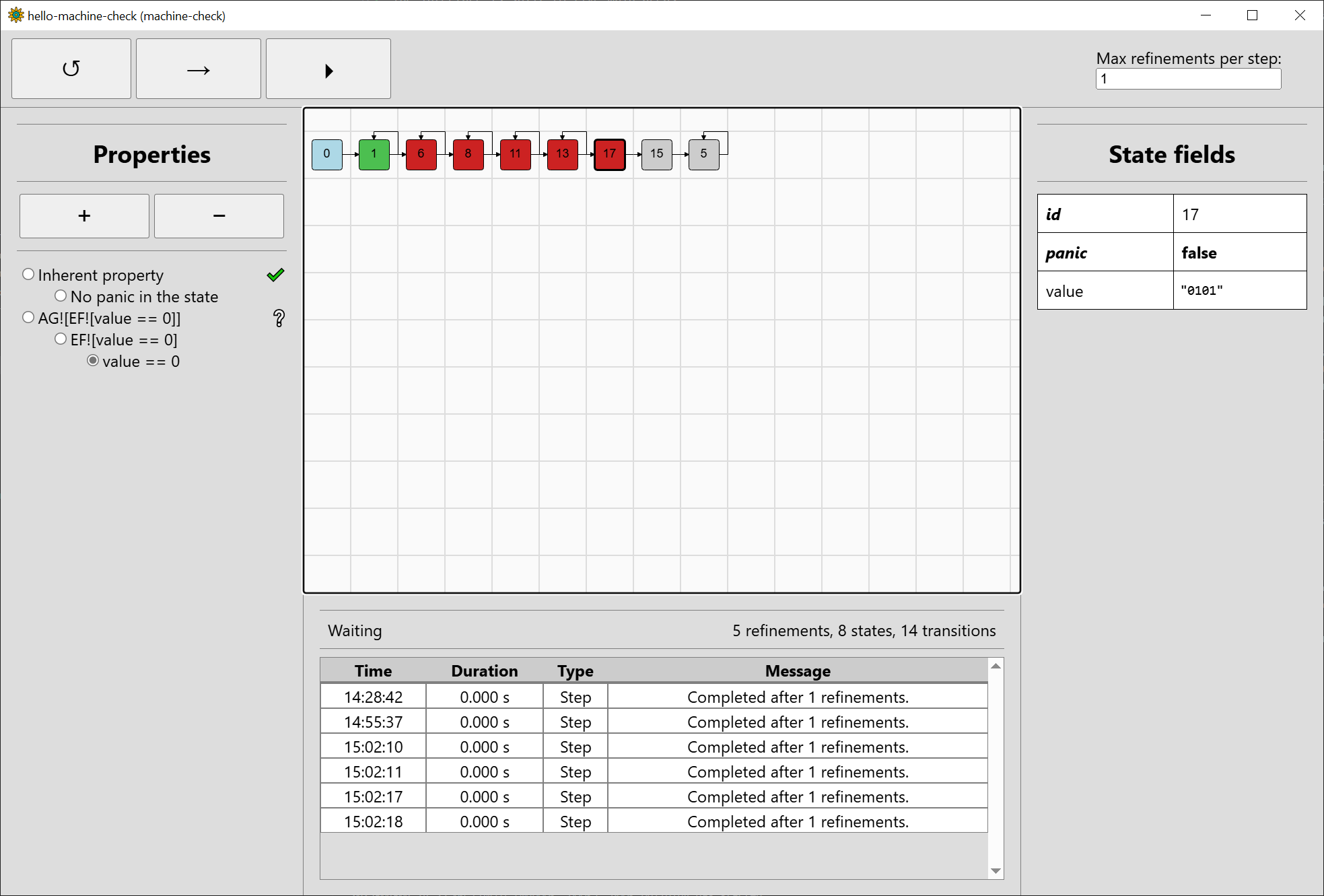
We see that value == 0 holds for the state #1 ("0000"), but does not hold for the states #6, #8, #11, #13, #17 ("0001", "0010", ..., "0101"), nor #15 ("01XX").
It is unknown whether it holds for #5 ("XXXX"), as this one may represent 0000 among others. We can switch to EF![value == 0] to
see how we fare there:
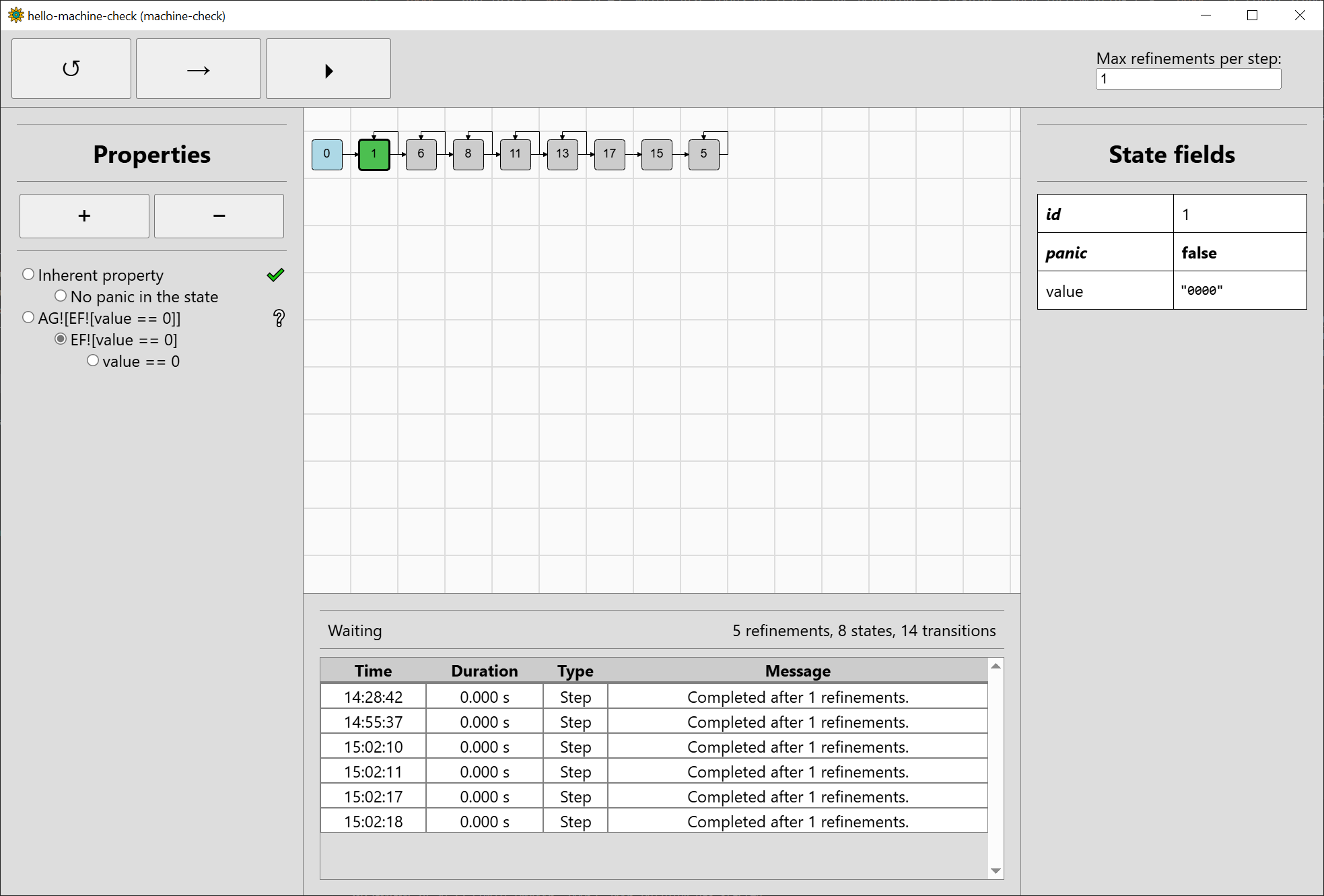
In #1, we can clearly choose a sequence of inputs such that value is eventually 0, since value is already 0 in the state. In the other states,
we do not have enough information to say anything yet.
As we now have a good idea how things work, run the verification to the end. Note that the refinements will be chosen according to the property to which the chosen subproperty belongs to (it does not make sense to refine based on the subproperty, but it is nice to be able to visualise our standing for it).
The final state space is a bit longer than previously:
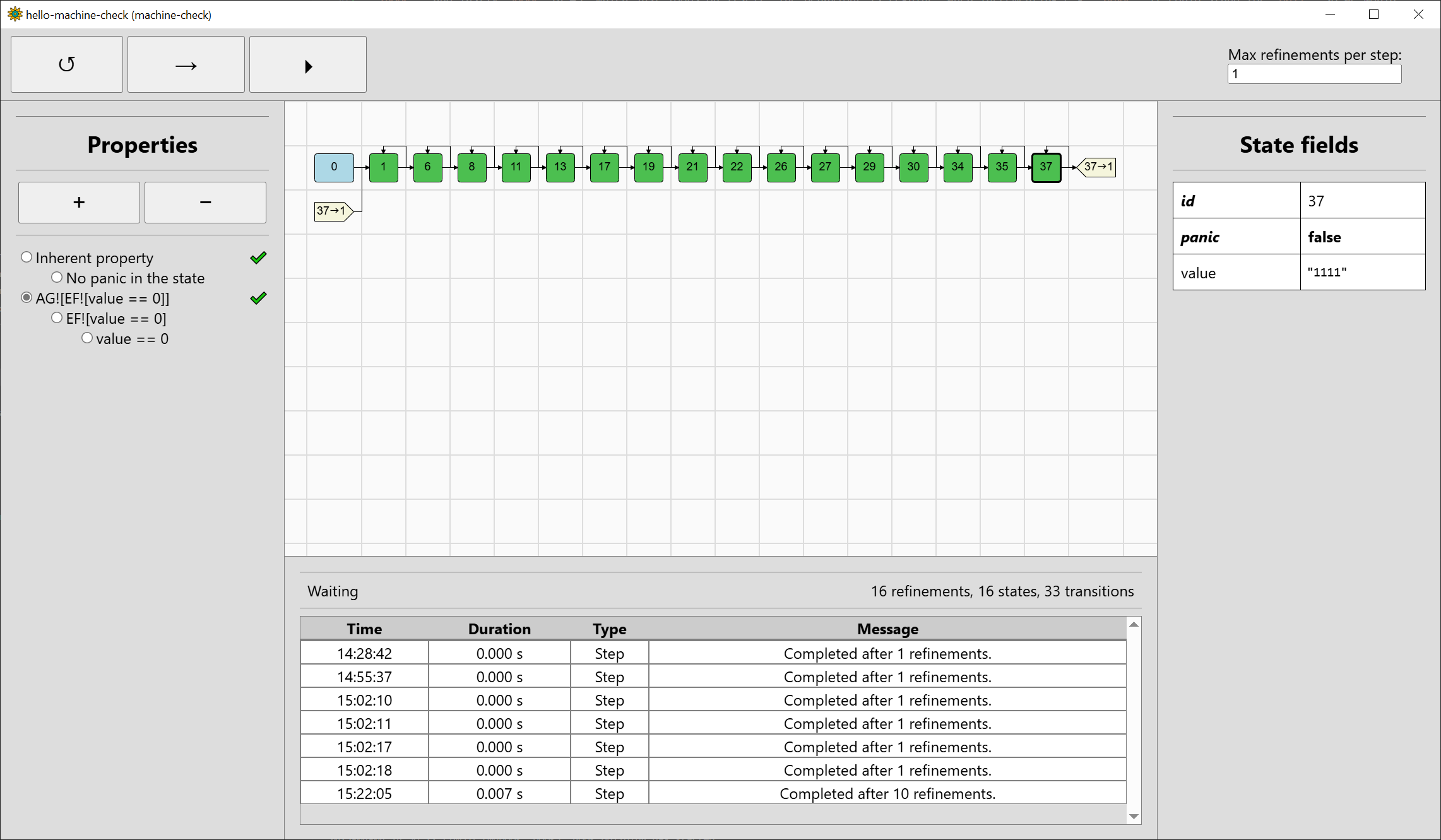
There is a before-unseen entity in the visualisation, graph references (light yellow) telling us about the the transition from #37 to #1. Since the state space graphs can be arbitrarily complex in general, only their spanning trees are drawn within the GUI visualisation, with references placed appropriately. Self-loops are an exception to the rule.
The property AG![EF![value == 0]] has been verified to hold, and you can inspect the subproperties to see if things match your intuition. Unfortunately,
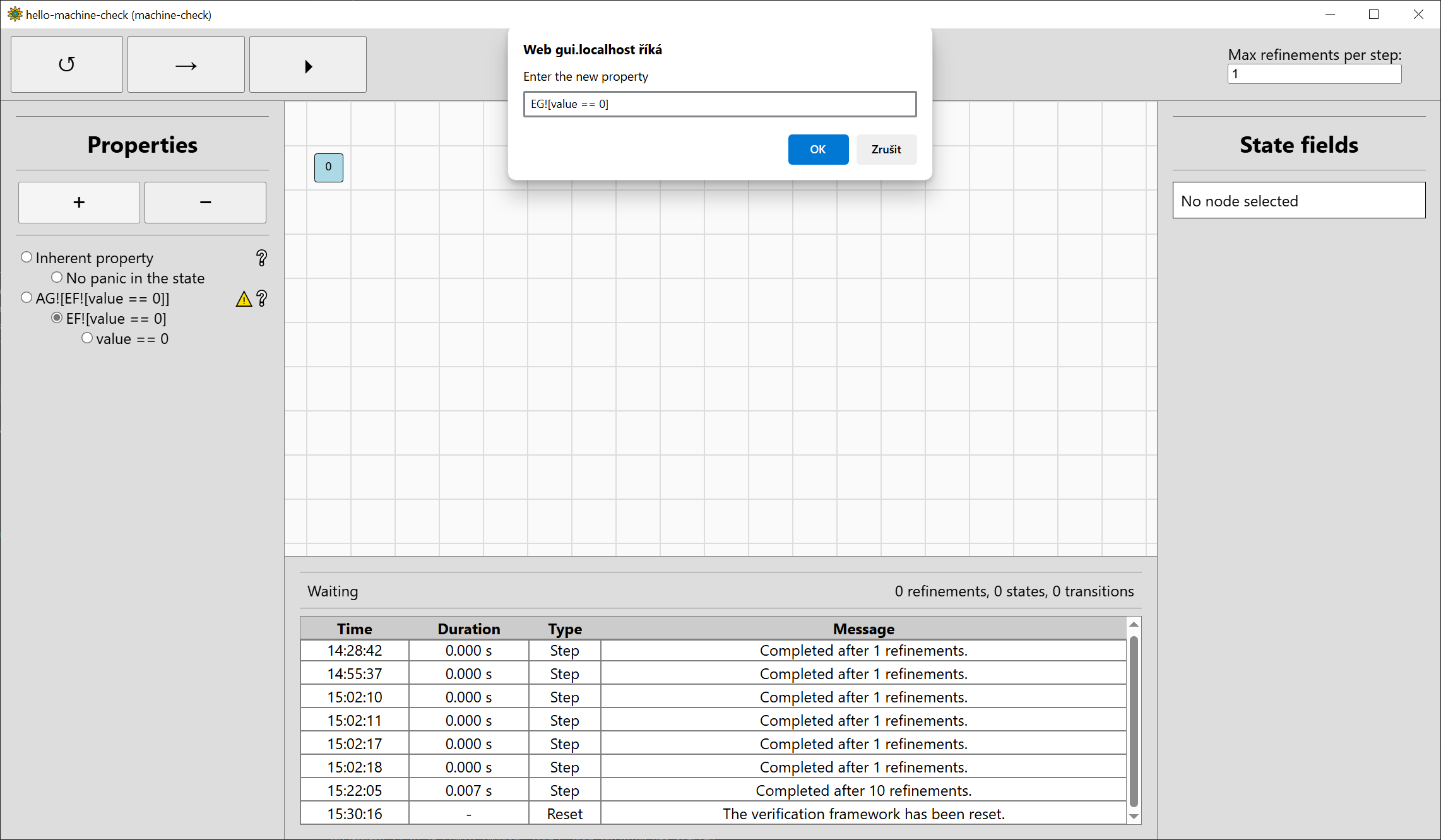
in this case, refinement did not really help us much. To see something where it would help, reset the verification and use the button to add a new
property (+) in the property bar. A dialog bar will pop up to enter a new property. You can also delete the selected non-inherent property by pressing
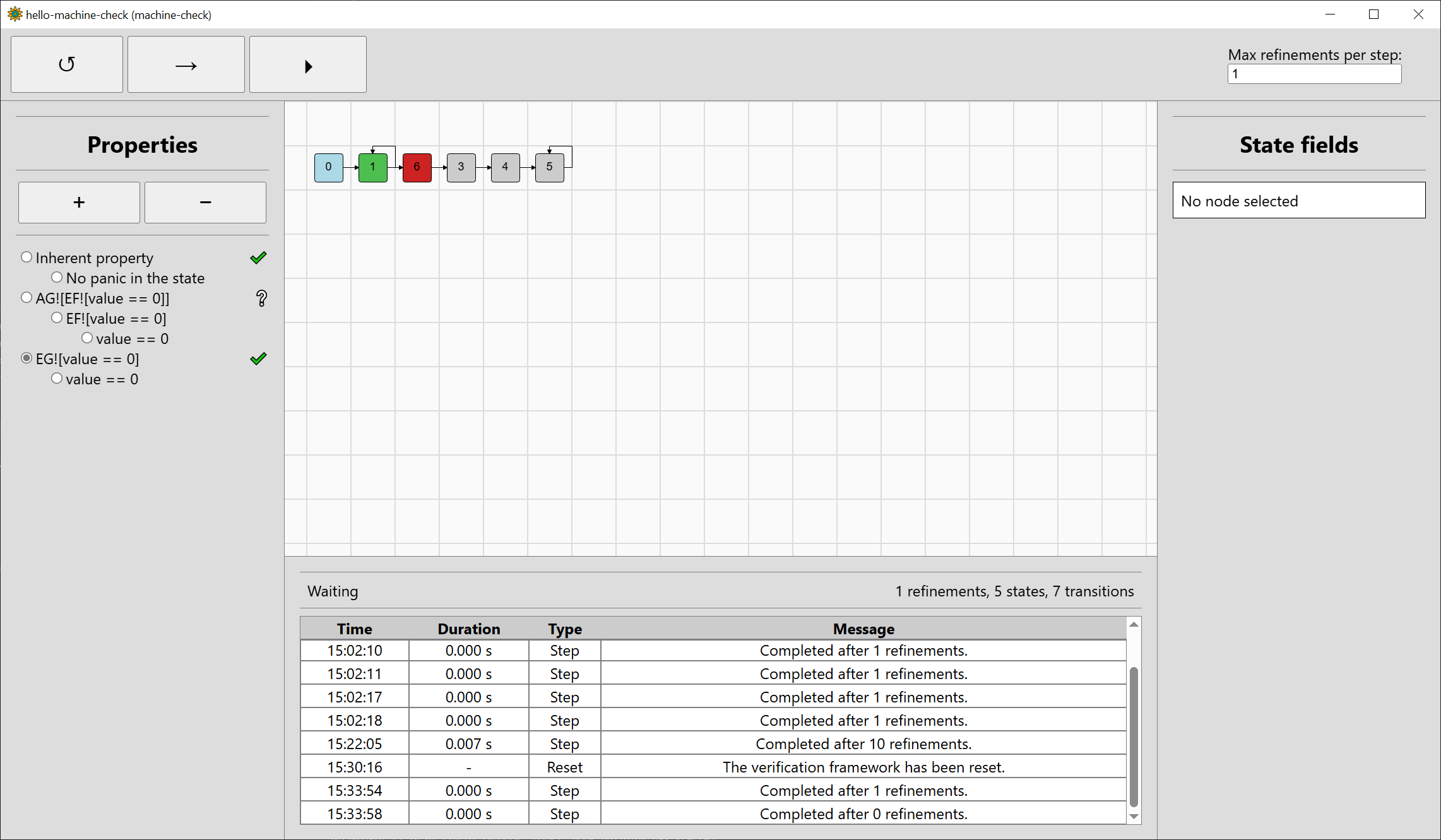
the remove-property button (-). Let's add a property EG![value == 0], i.e. there exists a sequence of inputs in which the value stays zero:
The property will be added to the end of the property bar, select it so it will be verified:
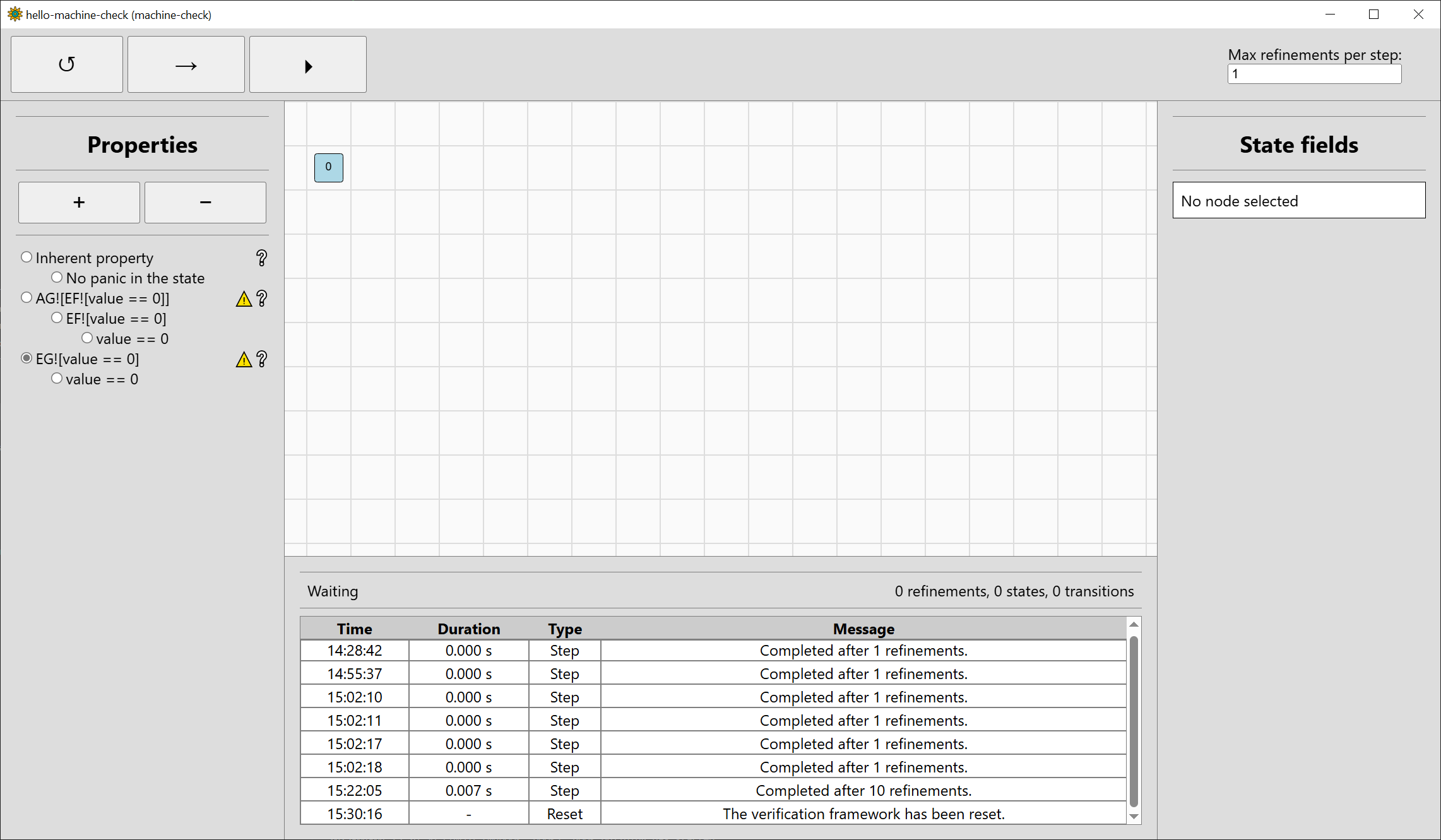
Step the verification twice, and the property will be verified. We only needed two refinements this time, and the final state space has just 5 states:
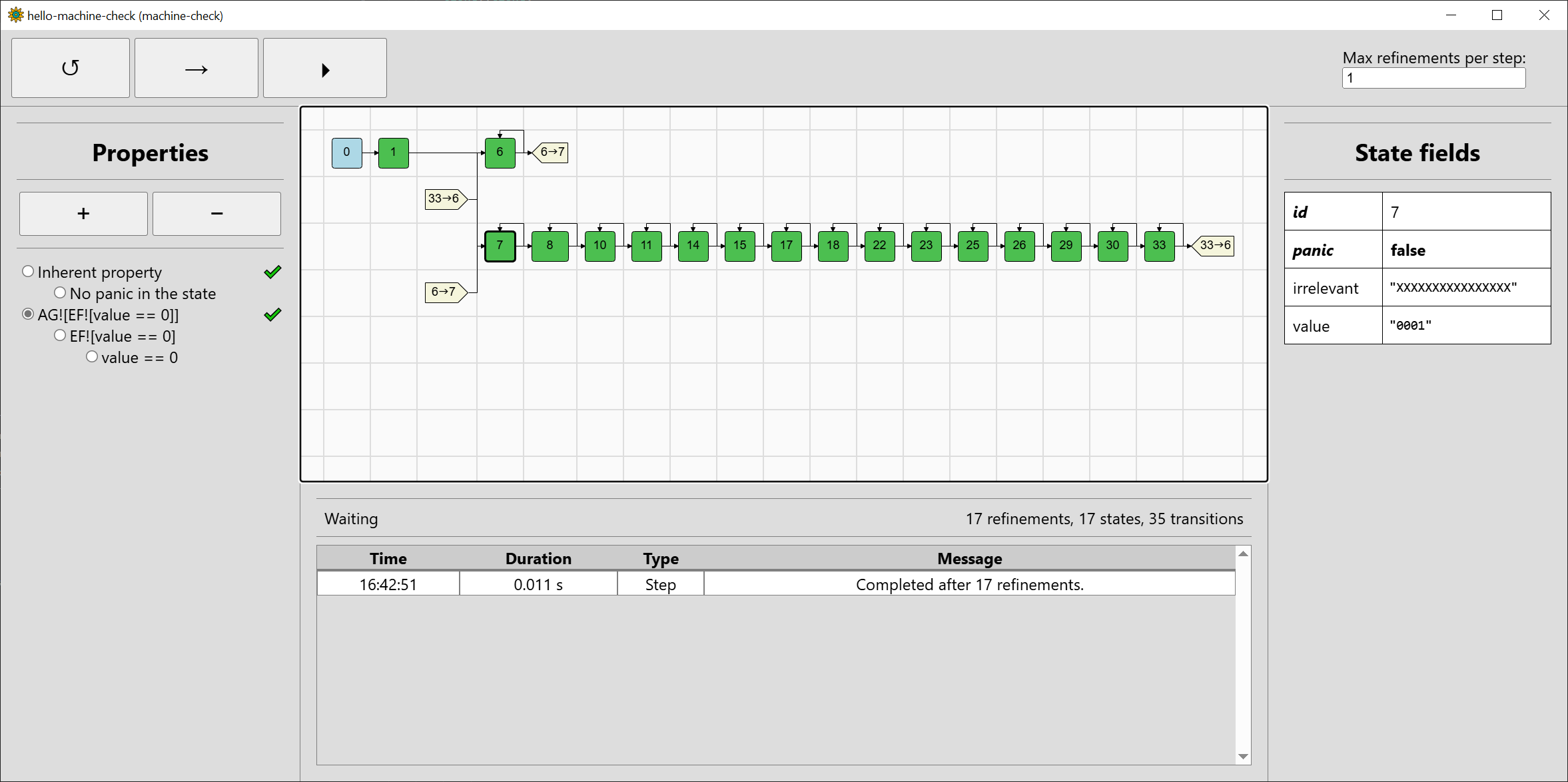
As we have seen, although the refinements used by machine-check can help, they can also make verification more complicated without a benefit. Fortunately, for complex systems such as machine-code systems, the benefits can be great. We can demonstrate that by making the input 32-bit, although only the lowest-bit input will be used after masking, and also adding an irrelevant field loaded in the next function to the value of another input:
#![allow(unused)] fn main() { #[derive(Clone, PartialEq, Eq, Hash, Debug)] pub struct Input { increment_value: Bitvector<32>, irrelevant_input: Bitvector<16>, } (...) #[derive(Clone, PartialEq, Eq, Hash, Debug)] pub struct State { value: Bitvector<4>, irrelevant: Bitvector<16>, } (...) fn init(&self, _input: &Input, _param: &Param) -> State { State { value: Bitvector::<4>::new(0), irrelevant: Bitvector::<16>::new(0), } } fn next(&self, state: &State, input: &Input, _param: &Param) -> State { let mut next_value = state.value; let increment_value_masked = input.increment_value & Bitvector::<32>::new(1); if increment_value_masked == Bitvector::<32>::new(1) { next_value = next_value + Bitvector::<4>::new(1); } State { value: next_value, irrelevant: input.irrelevant_input, } } }
The state space has become only slightly larger due to the field irrelevant being zeroed after initialisation and being fully unknown afterwards:
🛠️ The Graphical User Interface has been added machine-check 0.4, and there is still a lot of wonkiness. As with other parts of machine-check, further development is planned.
-
All states are graph nodes. The root node is a part of the graph has the initial states as its direct successors, but is not a state itself. ↩
Abstraction Domains
The ability of machine-check to verify complex systems is powered by two concepts: abstraction that lets us reason about more than just concrete states and refinement that reduces the amount of abstraction if we are not able to prove the property using it. You do not need to know about these domains for verification, but it is useful for inspecting the state spaces, which can be visualised using the GUI.
The abstraction technique used is existential abstraction, where we represent each state or input in an abstraction domain that limits the concrete possibilities. In machine-check, it is guaranteed at least one of these possibilities definitely exists.
For abstraction, machine-check currently uses the three-valued bit-vector (TVBV) domain, already seen in the chapter on GUI. This can be
combined with experimental dual-interval and equality domains using machine-check features Zdual_interval and Zeq_domain, respectively. These features
are also available in the systems provided in the next chapters.
Three-valued Bit-vector Domain
Already shown in the chapter on GUI, the idea of this domain is fairly simple: represent every bit of a state (or an input) by one of three values:
'0', meaning the bit is definitely 0,'1', meaning the bit is definitely 1,'X', meaning the bit may be 0 or 1, perhaps both (but we do not know if it actually can be both).
The bits are then displayed in the same manner as numbers in binary (most significant bit on the left, least significant bit on the right). This means that
e.g. "1X01" admits two possible concrete values, expressed in binary as 1001 and 1101 or in decimal as 9 or 13.
This domain is useful especially because it plays well with bitwise operations and, in particular, bitmasking. The main reason for introducing it first
in machine-check was that for embedded machine-code systems, reading input pins may be encoded in an instructions that reads a whole (e.g. 8-bit) port,
then masks it. Using the three-valued domain and reading e.g. bit 2 of some port, we can mask read "XXXXXXXX" to "00000X00", which will dramatically
shrink our state space and need for refinements.
Dual-Interval Domain
Intervals are a very straightforward abstraction: for example, if we have an interval [0,3], this means that the underlying possibilities are 0, 1, 2, and 3. Again, since this is an abstraction, not all of them must be actually present, we might have just e.g. 1 and 3.
The problem with normal intervals is that they do not handle signedness nicely: if we want to represent signed 0 and -1 using an unsigned interval, we can only use the full unsigned interval, making the abstraction fairly useless. This is problematic with digital systems since a lot of the time, the signedness is determined by the actual instruction or operation, not the data location itself.
We could use both signed and unsigned intervals, but this is rather awkward, as e.g. representing a 4-bit bitvector containing 4 and 12 (-4 in two's complement) would give us [4,12] ∩ [-4,4] (or, when represented as unsigned, [12,4]). Instead, we can use a dual-interval abstraction where we separately consider the possibilities for both values of sign bit, obtaining [4,4] ∪ [12,12]. This is done in machine-check, and the bounds are represented as if unsigned. Specially, if the dual-interval abstraction forms just a one unsigned interval, this interval is shown. For example, the abstract value for a 4-bit bitvector where the possibilities range from 3 to 9, [3,9] will be shown instead of [3,7] ∪ [8,9]. Specially, if only one value is possible, it will be shown instead.
While the dual-interval domain is not particularly useful for bitwise operations, it can precisely track arithmetic bounds.
🛠️ The increased precision brought by the dual-interval domain can lead to larger state spaces and longer verification times, which currently tends to be the case for most used test cases when the domain is used. Therefore, it is currently disabled by default until more clever strategies for state space generation and refinement are introduced that take it into account.
Combining the Domains
Both domains are used together when the Zdual_interval feature flag is used. This leads to bit-vector variables having values such as
"00001000" ∩ 8(where only one value is possible),"0000000100XXXX" ∩ [71, 72](where there exists a single unsigned interval),"XXXXXXXX" ∩ ([0, 126] ∪ [152, 255])(where there exist two intervals with different sign bit, which do not combine to a single unsigned interval).
Only the values admitted by both domains are possible. For example, "0000000100XXXX" ∩ [71, 72] admits only the possibilities 71 and 72.
Equality Domain
Also implemented is the equality domain, which tracks that two variables are equal to each other. It is an example of relational domains, which do not track just the values of one variable, but the relationships between more variables that limit the values.
The idea behind the implementation is to number variables such as input and parameters, and track the number through operations where the actual value does not change. This can allow us to determine other values as well. Let's illustrate this by the exclusive OR example. In the example, an input is copied to two distinct state variables, which are combined by an exclusive OR in the next state. We know that an exclusive OR of the same values produces a zero and the values are the same, but machine-check must refine down to single values by default, a worst-case scenario:
cargo run --release -- --property 'AG![xor_value == 0]'
(...)
[2025-10-28T19:21:59Z INFO machine_check] Starting verification.
[2025-10-28T19:21:59Z INFO machine_check::verify] Verifying the inherent property first.
[2025-10-28T19:21:59Z INFO machine_check::verify] The inherent property holds, proceeding to the given property.
[2025-10-28T19:21:59Z INFO machine_check::verify] Verifying the given property.
[2025-10-28T19:22:07Z INFO machine_check] Verification ended.
+---------------------------------+
| Result: HOLDS |
+---------------------------------+
| Refinements: 384 |
| Generated states: 687 |
| Final states: 64 |
| Generated transitions: 8367 |
| Final transitions: 4097 |
+---------------------------------+
However, the equality domain lets machine-check use the same reasoning as we just used, making the verification trivial:
cargo run --features machine-check/Zeq_domain -- --property 'AG![xor_value == 0]'
(...)
[2025-10-28T19:25:38Z INFO machine_check] Starting verification.
[2025-10-28T19:25:38Z INFO machine_check::verify] Verifying the inherent property first.
[2025-10-28T19:25:38Z INFO machine_check::verify] The inherent property holds, proceeding to the given property.
[2025-10-28T19:25:38Z INFO machine_check::verify] Verifying the given property.
[2025-10-28T19:25:38Z INFO machine_check] Verification ended.
+------------------------------+
| Result: HOLDS |
+------------------------------+
| Refinements: 0 |
| Generated states: 3 |
| Final states: 2 |
| Generated transitions: 3 |
| Final transitions: 3 |
+------------------------------+
In the GUI, the values of the two values and result are "XXXXXX" ∩ Eq(#0), "XXXXXX" ∩ Eq(#0), and "000000", respectively. The part Eq(#0) is an equality constraint that says the
variable is equal to a variable with tracking number #0. Within the equality domain, it is known that performing an exclusive OR of two variables with the same tracking number is equal
to zero, which makes verification of the example trivial.
It is also possible to use all three supported domains (three-valued bit-vector, dual-interval, equality) by enabling both features at the same time.
🛠️ The equality domain is currently disabled by default until more clever strategies for state space generation and refinement are introduced that take it into account.
machine-check-avr
Machine-check-avr provides a description of a machine-code system based on the AVR ATmega328P microcontroller, with some caveats. The description was created by transcribing the appropriate parts of the instruction set manual and the non-automotive ATmega328P datasheet.
The Intel HEX files used to load the program into the microcontroller can be provided as an argument to machine-check-avr: see the docs for details. This enables machine-code verification using machine-check.
For an example discussed in a presentation about a previous version of machine-check (the program on the slides is simplified for visibility), consider the following program written in C that can be used for calibration using binary search:
#define F_CPU 1000000
#include <avr/io.h>
#include <util/delay.h>
int main(void)
{
DDRC |= 0x01;
DDRD |= 0xFF;
while (1)
{
while ((PINC & 0x2) == 0) {}
// signify we are calibrating
PORTC |= 0x01;
// start with MSB of calibration
uint8_t search_bit = 7;
uint8_t search_mask = (1 << search_bit);
uint8_t search_val = search_mask;
while (1) {
// wait a bit
_delay_us(10);
// write the current search value
PORTD = search_val;
// wait a bit
_delay_us(10);
// get input value and compare it to desired
uint8_t input_value = PINB;
if ((input_value & 0x80) == 0) {
// input value lower than desired -> we should lower the calibration value
search_val &= ~search_mask;
}
if (search_bit == 0) {
// all bits have been set, stop
break;
}
search_bit -= 1;
// continue to next bit
search_mask >>= 1;
// update the search value with the next bit set
search_val |= search_mask;
}
// calibration complete, stop signifying that we are calibrating
PORTC &= ~0x01;
}
}
We can use machine-check-avr to find a verify a property in the compiled machine-code version of the program. We are doing binary search and setting PORTD according to search_val. Let us consider that, at any point in the program, we should be able to use some sequence of inputs to coerce PORTD to be zero.
Machine-check-avr can be installed as an executable using cargo:
cargo install machine-check-avr
Updating crates.io index
Installing machine-check-avr v0.7.0
Updating crates.io index
Locking 97 packages to latest compatible versions
(...)
Compiling machine-check-avr v0.7.0
Finished `release` profile [optimized] target(s) in 22.25s
warning: the following packages contain code that will be rejected by a future version of Rust: partitions v0.2.4
note: to see what the problems were, use the option `--future-incompat-report`, or run `cargo report future-incompatibilities --id 1`
Installing (...)\.cargo\bin\machine-check-avr.exe
Installed package `machine-check-avr v0.7.0` (executable `machine-check-avr.exe`)
The Intel HEX file obtained via compilation (that we can use to program the ATmega328P or provide to machine-check-avr) is not very self-explanatory (let us call it calibration_original.hex):
:100000000C9434000C943E000C943E000C943E0082
:100010000C943E000C943E000C943E000C943E0068
:100020000C943E000C943E000C943E000C943E0058
:100030000C943E000C943E000C943E000C943E0048
:100040000C943E000C943E000C943E000C943E0038
:100050000C943E000C943E000C943E000C943E0028
:100060000C943E000C943E0011241FBECFEFD8E04C
:10007000DEBFCDBF0E9440000C9466000C940000CF
:1000800087B1816087B98AB18FEF8AB9319BFECF82
:1000900088B1816088B980E890E827E033E03A953C
:1000A000F1F700008BB933E03A95F1F700001F99A2
:1000B00003C0392F30958323222321F021509695B8
:1000C000892BECCF88B18E7F88B9E0CFF894FFCF31
:00000001FF
We can try to verify the property, which we think should hold:
$ machine-check-avr --system-hex-file (...)\calibration_original.hex --property "AG![EF![PORTD == 0]]"
[2025-10-28T22:33:17Z INFO machine_check] Starting verification.
[2025-10-28T22:33:17Z INFO machine_check::verify] Verifying the inherent property first.
[2025-10-28T22:33:45Z INFO machine_check::verify] The inherent property holds, proceeding to the given property.
[2025-10-28T22:33:45Z INFO machine_check::verify] Verifying the given property.
[2025-10-28T22:33:48Z INFO machine_check] Verification ended.
+----------------------------------+
| Result: DOES NOT HOLD |
+----------------------------------+
| Refinements: 513 |
| Generated states: 14090 |
| Final states: 13059 |
| Generated transitions: 14603 |
| Final transitions: 13573 |
+----------------------------------+
This is caused by a bug in the program.
The problem is that PORTD is not updated to search_val at the end of search before the loop breaks, so the lowest bit is always set to one after each calibration. Let us fix this:
(...)
if (search_bit == 0) {
// all bits have been set, stop
// FIX BUG FOUND BY TOOL: write the end value
PORTD = search_val;
break;
}
(...)
Again, the new hex file does not tell us much, although it contains as much information as the microcontroller needs to execute the program (let's call it calibration_fixed.hex):
:100000000C9434000C943E000C943E000C943E0082
:100010000C943E000C943E000C943E000C943E0068
:100020000C943E000C943E000C943E000C943E0058
:100030000C943E000C943E000C943E000C943E0048
:100040000C943E000C943E000C943E000C943E0038
:100050000C943E000C943E000C943E000C943E0028
:100060000C943E000C943E0011241FBECFEFD8E04C
:10007000DEBFCDBF0E9440000C9467000C940000CE
:1000800087B1816087B98AB18FEF8AB9319BFECF82
:1000900088B1816088B980E890E827E033E03A953C
:1000A000F1F700008BB933E03A95F1F700001F99A2
:1000B00003C0392F30958323211105C08BB988B136
:1000C0008E7F88B9E3CF21509695892BE7CFF8949E
:0200D000FFCF60
:00000001FF
We'll verify that the property now holds:
$ machine-check-avr --system-hex-file (...)\calibration_fixed.hex --property "AG![EF![PORTD == 0]]"
[2025-10-28T22:35:01Z INFO machine_check] Starting verification.
[2025-10-28T22:35:01Z INFO machine_check::verify] Verifying the inherent property first.
[2025-10-28T22:35:30Z INFO machine_check::verify] The inherent property holds, proceeding to the given property.
[2025-10-28T22:35:30Z INFO machine_check::verify] Verifying the given property.
[2025-10-28T22:35:42Z INFO machine_check] Verification ended.
+----------------------------------+
| Result: HOLDS |
+----------------------------------+
| Refinements: 513 |
| Generated states: 14090 |
| Final states: 13059 |
| Generated transitions: 14603 |
| Final transitions: 13573 |
+----------------------------------+
Perfect. Being happy with the result, we can uninstall the executable:
$ cargo uninstall machine-check-avr
Removing (...)\.cargo\bin\machine-check-avr.exe
💡️ Generally, the major problem with verification of complex systems such as machine-code systems is that machine-check may not choose the refinements correctly and the time or memory needed for verification will be unacceptable. This will depend on the program and the cleverness of machine-check when using the chosen strategy, and can be investigated using the GUI.
🛠️ Currently, the ease of use of machine-check-avr leaves something to be desired: for example, if we want to verify a property depending on some line in the program source code, we have to obtain the mapping of the source-code line to the the value of the Program Counter (
PC) ourselves. In the future, machine-check-avr could be extended to obtain this information automatically from a file with debug information.
machine-check-hw
Machine-check-hw is a tool for verifying hardware systems in the Btor2 specification format. It translates the system to the subset of Rust supported by machine-check, compiles the resulting Rust package using Cargo or rustc together with verification logic, and runs the executable.
To install machine-check-hw, execute
$ cargo install machine-check-hw
The next step is optional, but useful for reasonable performance. To avoid downloading all of the libraries for every machine compilation, first run
$ machine-check-hw prepare
This will create a new directory machine-check-preparation in the executable installation directory which contains the needed libraries, speeding up compilation and avoiding subsequent downloads, allowing offline verification.
In case something goes wrong with preparation, you can revert back to no-preparation mode by running
$ machine-check-hw prepare --clean
Verification
It is possible to verify various properties of Btor2 systems using machine-check-hw. The inherent property is also verified during property verification: there are no explicit panics created from the Btor2 files, but division and remainder by zero violate the inherent property.
Safety
To actually verify something, we can obtain a simple Btor2 system, e.g. beads.btor2 from machine-check-hw examples. By pointing machine-check-hw to a Btor2 file, it can verify the safety of the system, as specified in the Btor2 file, with a property AG![safe == 1], which uses a special field safe:
$ machine-check-hw verify ./beads.btor2 --property 'AG![safe == 1]'
[2025-10-28T22:38:52Z INFO machine_check_compile::verify] Transcribing the system into a machine.
[2025-10-28T22:38:52Z INFO machine_check_compile::verify] Building a machine verifier.
[2025-10-28T22:38:58Z INFO machine_check_compile::verify] Executing the machine verifier.
[2025-10-28T22:38:58Z INFO machine_check] Starting verification.
[2025-10-28T22:38:58Z INFO machine_check::verify] Verifying the inherent property first.
[2025-10-28T22:38:58Z INFO machine_check::verify] The inherent property holds, proceeding to the given property.
[2025-10-28T22:38:58Z INFO machine_check::verify] Verifying the given property.
[2025-10-28T22:38:58Z INFO machine_check] Verification ended.
[2025-10-28T22:38:58Z INFO machine_check_compile::verify] Stats: Stats { transcription_time: Some(0.0008279), build_time: Some(6.1309139), execution_time: Some(0.0952816), prepared: Some(true) }
[2025-10-28T22:38:58Z INFO machine_check_hw::verify] Used 3 states and 0 refinements.
[2025-10-28T22:38:58Z INFO machine_check_hw::verify] Reached conclusion: true
Recovery
We can also verify the property of whether the system recovers to its initial inputs (for the state nodes where they are specified). This can be done using the property AG![EF![eq_init == 1]], which uses a special field eq_init:
$ machine-check-hw verify ./beads.btor2 --property 'AG![EF![eq_init == 1]]'
(...)
[2025-10-28T22:39:13Z INFO machine_check_compile::verify] Stats: Stats { transcription_time: Some(0.0007483), build_time: Some(5.8962471), execution_time: Some(0.0995338), prepared: Some(true) }
[2025-10-28T22:39:13Z INFO machine_check_hw::verify] Used 5 states and 5 refinements.
[2025-10-28T22:39:13Z INFO machine_check_hw::verify] Reached conclusion: true
State properties
Instead of verifying reachability properties in the file, we can verify custom Computation Tree Logic properties on its states. For example, the beads.btor2 has three states (100, 200, 300) which determine bead positions and a single input. If the input is 0, the beads stay in their positions, if it is 1, they move to the next position. Machine-check-hw creates a state variable node_X for each state node identifier X in the state. This means that we can verify various properties on the states.
$ machine-check-hw verify ./beads.btor2 --property 'EG![node_200 == 1]'
(...)
[2025-10-28T22:39:50Z INFO machine_check_compile::verify] Stats: Stats { transcription_time: Some(0.0006642), build_time: Some(5.8038741), execution_time: Some(0.0949872), prepared: Some(true) }
[2025-10-28T22:39:50Z INFO machine_check_hw::verify] Used 3 states and 0 refinements.
[2025-10-28T22:39:50Z INFO machine_check_hw::verify] Reached conclusion: false
The conclusion is false, i.e. there does not exist a path where the bead is always in the second position.
$ machine-check-hw verify ./beads.btor2 --property 'EF![EG![node_200 == 1]]'
(...)
[2025-10-28T22:39:27Z INFO machine_check_compile::verify] Stats: Stats { transcription_time: Some(0.000709), build_time: Some(5.914955), execution_time: Some(0.0975522), prepared: Some(true) }
[2025-10-28T22:39:27Z INFO machine_check_hw::verify] Used 6 states and 3 refinements.
[2025-10-28T22:39:27Z INFO machine_check_hw::verify] Reached conclusion: true
The conclusion is true, i.e. there exists a future where the bead moves to second position and then stays there.
$ machine-check-hw verify ./beads.btor2 --property 'AF![node_200 == 1]'
(...)
[2025-10-28T22:40:05Z INFO machine_check_compile::verify] Stats: Stats { transcription_time: Some(0.0008921), build_time: Some(6.03603), execution_time: Some(0.0960045), prepared: Some(true) }
[2025-10-28T22:40:05Z INFO machine_check_hw::verify] Used 5 states and 1 refinements.
[2025-10-28T22:40:05Z INFO machine_check_hw::verify] Reached conclusion: false
The conclusion is false, i.e. we cannot be sure that the bead will ever move to the second position.
$ machine-check-hw verify ./beads.btor2 --property 'EU![node_100 == 1, node_200 == 1]'
(...)
[2025-10-28T22:40:19Z INFO machine_check_compile::verify] Stats: Stats { transcription_time: Some(0.0010942), build_time: Some(5.7909552), execution_time: Some(0.0959956), prepared: Some(true) }
[2025-10-28T22:40:19Z INFO machine_check_hw::verify] Used 5 states and 1 refinements.
[2025-10-28T22:40:19Z INFO machine_check_hw::verify] Reached conclusion: true
The conclusion is true, i.e. there exists a path where the the bead is in the first position until it is in the second position, and the second position is reached.
$ machine-check-hw verify ./beads.btor2 --property 'AU![node_100 == 1, node_200 == 1]'
(...)
[2025-10-28T22:40:37Z INFO machine_check_compile::verify] Stats: Stats { transcription_time: Some(0.001045), build_time: Some(5.9079046), execution_time: Some(0.0968339), prepared: Some(true) }
[2025-10-28T22:40:37Z INFO machine_check_hw::verify] Used 5 states and 1 refinements.
[2025-10-28T22:40:37Z INFO machine_check_hw::verify] Reached conclusion: false
The conclusion is false, i.e. the bead stops being in the first position before being in the second position (which we know is not possible), or the second position is never reached (which is possible if it stays in the first position forever).
$ machine-check-hw verify ./beads.btor2 --property 'AG![!(node_200 == 1) || EX![node_300 == 1]]'
(...)
[2025-10-28T22:40:51Z INFO machine_check_compile::verify] Stats: Stats { transcription_time: Some(0.0006929), build_time: Some(5.9525331999999995), execution_time: Some(0.096231), prepared: Some(true) }
[2025-10-28T22:40:51Z INFO machine_check_hw::verify] Used 5 states and 5 refinements.
[2025-10-28T22:40:51Z INFO machine_check_hw::verify] Reached conclusion: true
$ machine-check-hw verify ./beads.btor2 --property 'AG![!(node_200 == 1) || EX![node_100 == 1]]'
(...)
[2025-10-28T22:41:05Z INFO machine_check_compile::verify] Stats: Stats { transcription_time: Some(0.0006606), build_time: Some(5.8645651), execution_time: Some(0.0946764), prepared: Some(true) }
[2025-10-28T22:41:05Z INFO machine_check_hw::verify] Used 5 states and 1 refinements.
[2025-10-28T22:41:05Z INFO machine_check_hw::verify] Reached conclusion: false
The conclusions mean that the bead being in the second position implies that the bead can move to the third position in the next state. However, it cannot move to the first position so quickly.
Limitations
The Btor2 files must contain only bit-vectors (no arrays) with at most 64 bits. Only safety is supported within Btor2, with no support for fairness, invariant constraints, and justice properties.
It is currently not feasible to verify very complex hardware systems verifiable by state-of-the-art hardware verificaiton tools. However, unlike many such tools, machine-check does not focus on specific properties such as safety, allowing verification of arbitrary Computation Tree Logic properties.
💡️ The HWMCC competition compares the state-of-the-art Btor2 verification tools.
Parametric Systems
Often, we do not have complete information about how a system behaves, or we intentionally do not want to describe the behaviour as it could be too complex and not relevant to the properties we want to verify.
For example, we might have a microcontroller program which uses a serial input peripheral where the range of possibly read values depends on some complex configuration. It is not completely correct to treat these as inputs since the property verification assumes all inputs can occur. As such, we might verify that a property holds due to one of the inputs, even though this input never occurs in practice.
We already have one way to handle these kinds of uncertainties: panic when the result could depend on them. This, however, can be too coarse, as some properties can hold or not hold independently of this uncertainty. As such, machine-check supports parametric verification, where instead of verifying whether a property holds in a single system, we verify whether it holds in a set of systems. This gives us three possibilities for verification results:
- Does not hold in any of the systems,
- Holds in some and does not hold in others,
- Holds in all of the systems.
If we verify that the property holds or it does not for all systems, it means that we can safely ignore the behaviour hidden by the parameter. If we verify that it only holds in some, it can also be a cause for concern if this does not match our expectations.
Let's look at the simple parametric example for machine-check:
#![allow(unused)] fn main() { (...) #[derive(Clone, PartialEq, Eq, Hash, Debug)] pub struct Input { value: Unsigned<4>, } #[derive(Clone, PartialEq, Eq, Hash, Debug)] pub struct Param { max_value: Unsigned<4>, } #[derive(Clone, PartialEq, Eq, Hash, Debug)] pub struct State { value: Unsigned<4>, max_value: Unsigned<4>, } #[derive(Clone, PartialEq, Eq, Hash, Debug)] pub struct System {} impl ::machine_check::Machine for System { type Input = Input; type State = State; type Param = Param; fn init(&self, _input: &Input, param: &Param) -> State { State { max_value: param.max_value, value: Unsigned::<4>::new(0), } } fn next(&self, state: &State, input: &Input, _param: &Param) -> State { let mut value = input.value; if value >= state.max_value { value = state.max_value; } State { value, max_value: state.max_value, } } } (...) }
For understandability, this example only corresponds to 16 actual parametrised systems: the field max_value of Param is copied to max_value in state during initialisation and remains the same throughout time.
The system loads a value from the input during the next state computation, making sure the value stored in the state is at most max_value. As such, we have a system where the value stored in the state can only be 0
(since max_value is 0), a system where the value can be 0 or 1 (since max_value is 1), and so on until the system where the value can range from 0 to 15. We can now verify some properties on this:
$ cargo run -- --property 'AG![value == 0]'
Finished `dev` profile [unoptimized + debuginfo] target(s) in 2.47s
warning: the following packages contain code that will be rejected by a future version of Rust: partitions v0.2.4
note: to see what the problems were, use the option `--future-incompat-report`, or run `cargo report future-incompatibilities --id 2`
Running `target\debug\hello-machine-check.exe --property "AG![value == 0]"`
[2025-10-28T22:26:48Z INFO machine_check] Starting verification.
[2025-10-28T22:26:48Z INFO machine_check::verify] Verifying the inherent property first.
[2025-10-28T22:26:48Z INFO machine_check::verify] The inherent property holds, proceeding to the given property.
[2025-10-28T22:26:48Z INFO machine_check::verify] Verifying the given property.
[2025-10-28T22:26:48Z INFO machine_check] Verification ended.
+-----------------------------------+
| Result: DEPENDS ON PARAMETERS |
+-----------------------------------+
| Refinements: 5 |
| Generated states: 69 |
| Final states: 33 |
| Generated transitions: 96 |
| Final transitions: 50 |
+-----------------------------------+
We can reason about the result as follows: if max_value is 0, then the only possible path to take is all-zeros, so it will hold that the value is zero globally on all paths. On the other hand, if max_value is larger,
we can take a path where value is 1 somewhere, so the property does not hold.
Some properties, however, hold or not independently on the parameter:
cargo run -- --property 'AF![as_unsigned(value) > 0]'
Finished `dev` profile [unoptimized + debuginfo] target(s) in 0.11s
warning: the following packages contain code that will be rejected by a future version of Rust: partitions v0.2.4
note: to see what the problems were, use the option `--future-incompat-report`, or run `cargo report future-incompatibilities --id 2`
Running `target\debug\hello-machine-check.exe --property "AF![as_unsigned(value) > 0]"`
[2025-10-28T22:27:03Z INFO machine_check] Starting verification.
[2025-10-28T22:27:03Z INFO machine_check::verify] Verifying the inherent property first.
[2025-10-28T22:27:03Z INFO machine_check::verify] The inherent property holds, proceeding to the given property.
[2025-10-28T22:27:03Z INFO machine_check::verify] Verifying the given property.
[2025-10-28T22:27:03Z INFO machine_check] Verification ended.
+--------------------------------+
| Result: DOES NOT HOLD |
+--------------------------------+
| Refinements: 64 |
| Generated states: 368 |
| Final states: 151 |
| Generated transitions: 784 |
| Final transitions: 287 |
+--------------------------------+
No matter the max_value, we can always take the path where the state value is zero forever, which disproves the property. See the parametric example for examples of more properties.
It is also possible to use the parameters in the next state computation function: in that case, each time instant has its own "fresh" parameter argument independent of others instead of the single unchanging max_value in the example, essentially producing an infinite number of systems fulfilling the description.
🛠️ The ability to verify with parameters is currently somewhat experimental. While the abstraction-refinement framework used by machine-check is used even for abstracting and refining parameters, uses such as the above example are currently not a very good fit due to the current absence of relational domains more powerful than equality.
System Hierarchy Checking
We can also use parametric systems with a different thought process. Consider that you are given a specification in form of a system which has some unspecified parts, and an implementation that should "fill the spots" while retaining the behaviours of the specification system. Then, you can actually think of the specification system as a system that is parametrised by variables determining the unspecified values.
Let's look at the simple system hierarchy example for machine-check, where a specification of a system performing an unsigned division of two numbers says that the result of division by zero must be either 0 (as in e.g. some AVR processors) or the unsigned maximum (as in e.g. RISC-V), but leaves the implementation free to choose one of them. The specification result is represented by specified_value, the implementation result as impl_value, and the relevant computation is as follows (param.unspecified is a signed single-bit parameter, which will be extended either to 0 or -1, i.e. the maximum unsigned value):
#![allow(unused)] fn main() { if input.divisor != Unsigned::<4>::new(0) { specified_value = input.dividend / input.divisor; impl_value = input.dividend / input.divisor; } else { specified_value = Into::<Unsigned<4>>::into(Ext::<4>::ext(param.unspecified)); impl_value = self.division_by_zero_result; } }
Running the example normally (add import clap = { version = "4.4.6", features = ["derive"] } to your Cargo.toml if you are going to copy the example to your package), the default system implementation has self.division_by_zero_result set to 0. Running to check that the values will be the same, we get:
cargo run -- --property 'AG![specified_value == impl_value]'
(...)
[2025-10-28T22:28:20Z INFO machine_check] Starting verification.
[2025-10-28T22:28:20Z INFO machine_check::verify] Verifying the inherent property first.
[2025-10-28T22:28:20Z INFO machine_check::verify] The inherent property holds, proceeding to the given property.
[2025-10-28T22:28:20Z INFO machine_check::verify] Verifying the given property.
[2025-10-28T22:28:20Z INFO machine_check] Verification ended.
+-----------------------------------+
| Result: DEPENDS ON PARAMETERS |
+-----------------------------------+
| Refinements: 9 |
| Generated states: 44 |
| Final states: 17 |
| Generated transitions: 1057 |
| Final transitions: 34 |
+-----------------------------------+
This actually makes sense in the context: if the parameter (unspecified value) is 0, then the implementation and specification system with that parameter are the same. If not, they are different. As such, the specification system is hierarchically "above" the implementation. On the other hand, we can pass the parameter --system-wrong-div-by-zero to force the division-by-zero result to 1, which is not allowed:
cargo run -- --property 'AG![specified_value == impl_value]' --system-wrong-div-by-zero
(...)
[2025-10-28T22:28:43Z INFO machine_check] Starting verification.
[2025-10-28T22:28:43Z INFO machine_check::verify] Verifying the inherent property first.
[2025-10-28T22:28:43Z INFO machine_check::verify] The inherent property holds, proceeding to the given property.
[2025-10-28T22:28:43Z INFO machine_check::verify] Verifying the given property.
[2025-10-28T22:28:43Z INFO machine_check] Verification ended.
+-------------------------------+
| Result: DOES NOT HOLD |
+-------------------------------+
| Refinements: 5 |
| Generated states: 14 |
| Final states: 6 |
| Generated transitions: 71 |
| Final transitions: 12 |
+-------------------------------+
This says that there is no valuation of the parameters such that the implementation would correspond to the specification system. As such, we learned that the implementation hierarchically has no relation with the specification, which violates our expectations.
🛠️ Checking the hierarchical relationship of two parametric systems is currently not supported.
μ-calculus Properties
While the Computation Tree Logic is relatively simple to use, there are interesting properties that cannot be expressed using it. Machine-check supports a much more powerful temporal logic: propositional (also called modal) μ-calculus. In fact, even the CTL properties are internally translated to μ-calculus before they are used for model checking, and the only thing needed to unlock the power of μ-calculus are two new macro-style operators.
Local Reasoning
Compared to CTL, μ-calculus properties are described using local reasoning, which is converted to global reasoning using the operators μ and ν. These correspond to computing the least and the greatest fixed points, respectively, so the machine-check macros for them are lfp! and gfp!, respectively. Let's look at what this means by examining the CTL operators first.
The CTL operator AG![a], meaning "on all paths, globally, a holds", can be rewritten to gfp![Z, a && AX![Z]]. This makes the identifier Z a fixpoint variable within the second argument of gfp!. We can think of Z as a variable that has some value for every state. The computation will proceed as follows:
Zwill be initialised to be true in all states.- In the first computation iteration, since
Zis true everywhere,AX![Z]is also be true everywhere and we only need to considera. Thus, at the end of the iteration,Zwill become false for all states whereadoes not hold. - In subsequent computation iterations,
Zwill change in the states directly preceding the states whereZchanged to false. - This will propagate further and further until there are no longer any states where the iteration changes the valuation of
Zin any state.
The computation will only end when we reach the fixed point, where the iteration produces nothing new; then, Z is the computed valuation of states. This will produce the same result as AG![a] should: all states which have some (arbitrarily far-away) successor where a does not hold will have the valuation false, while all others will have the valuation true since nothing has happened to change it.
For another example, the operator AF![a], meaning "on all paths, eventually (now or in the future), a holds", lfp![Z, a || AX![Z]]. This is the least fixed point (μ), which sets Z to false in all states at first, then sets it true in the states where a holds, and then propagates the true valuations backward.
The full table of translations for CTL operators is:
EG![a] = gfp![Z, a && EX![Z]]
AG![a] = gfp![Z, a && AX![Z]]
EF![a] = lfp![Z, a || EX![Z]]
AF![a] = lfp![Z, a || AX![Z]]
ER![a, b] = gfp![Z, b && (a || EX![Z])]
AR![a, b] = gfp![Z, b && (a || AX![Z])]
EU![a, b] = lfp![Z, b || (a && EX![Z])]
AU![a, b] = lfp![Z, b || (a && AX![Z])]
Note how the E/A path quantifier only affects the choice of EX!/AX!, while the choice between G/F or R/U selects the type of the fixed point. As the CTL operators may be used as-is in machine-check, the most useful thing about the translations above is that we can get some intuition about how to build properties not expressible in CTL.
Example: Holds in Even Positions
The example mu_even in machine-check demonstrates a system with an interesting property not expressible in Computation Tree Logic, nor the related Linear Tree Logic and CTL*: a property holding at even time instants. The value is computed as follows:
#![allow(unused)] fn main() { (...) let currently_odd_position = state.odd_position + Bitvector::<1>::new(1); // if the current position is even, set the value to 0 // if the current position is odd, set the value to the input value let mut value = Bitvector::<8>::new(0); if currently_odd_position == Bitvector::<1>::new(1) { value = input.value; } (...) }
We want to know if the value is definitely zero in even time instants, while it can be whatever in odd time instants. The solution in μ-calculus is simple: use the property gfp![Z, value == 0 && AX![AX![Z]]]. This means that even if the value is nonzero in an odd time instant, this will only be propagated backwards two system steps at a time, so it cannot impact the valuation of the property at time zero. Running verification:
$ cargo run -- --property 'gfp![Z, value == 0 && AX![AX![Z]]]'
Finished `dev` profile [unoptimized + debuginfo] target(s) in 0.10s
warning: the following packages contain code that will be rejected by a future version of Rust: partitions v0.2.4
note: to see what the problems were, use the option `--future-incompat-report`, or run `cargo report future-incompatibilities --id 2`
Running `target\debug\hello-machine-check.exe --property "gfp![Z, value == 0 && AX![AX![Z]]]"`
[2025-10-28T22:29:40Z INFO machine_check] Starting verification.
[2025-10-28T22:29:40Z INFO machine_check::verify] Verifying the inherent property first.
[2025-10-28T22:29:40Z INFO machine_check::verify] The inherent property holds, proceeding to the given property.
[2025-10-28T22:29:40Z INFO machine_check::verify] Verifying the given property.
[2025-10-28T22:29:40Z INFO machine_check] Verification ended.
+------------------------------+
| Result: HOLDS |
+------------------------------+
| Refinements: 0 |
| Generated states: 3 |
| Final states: 2 |
| Generated transitions: 3 |
| Final transitions: 3 |
+------------------------------+
Variations of the local reasoning could be used to construct other properties of interest, e.g. checking only every fifth state from some point, checking using existential next operators, etc.
Example: Infinitely Often
The example mu_infinitely_often demonstrates the ability of the μ-calculus to verify a property that cannot be expressed in Computation Tree Logic, but can be in Linear Time Logic: that something happens infinitely often. This can be expressed as FG in LTL. The similar property AFAG in CTL describes a different concept, that something happens eventually forever. The example gives the standard system that reveals the difference between the two: in state 0 where p holds, we have a choice between looping and going to state 1 where p does not hold. From state 1, the only possible transition is to state 2 where p holds again, and where the system loops forever.
Let us first verify the CTL property eventually forever:
$ cargo run -- --property 'AF![AG![p == 1]]'
Finished `dev` profile [unoptimized + debuginfo] target(s) in 1.99s
warning: the following packages contain code that will be rejected by a future version of Rust: partitions v0.2.4
note: to see what the problems were, use the option `--future-incompat-report`, or run `cargo report future-incompatibilities --id 2`
Running `target\debug\hello-machine-check.exe --property "AF![AG![p == 1]]"`
[2025-10-28T22:30:26Z INFO machine_check] Starting verification.
[2025-10-28T22:30:26Z INFO machine_check::verify] Verifying the inherent property first.
[2025-10-28T22:30:26Z INFO machine_check::verify] The inherent property holds, proceeding to the given property.
[2025-10-28T22:30:26Z INFO machine_check::verify] Verifying the given property.
[2025-10-28T22:30:26Z INFO machine_check] Verification ended.
+------------------------------+
| Result: DOES NOT HOLD |
+------------------------------+
| Refinements: 1 |
| Generated states: 8 |
| Final states: 3 |
| Generated transitions: 9 |
| Final transitions: 5 |
+------------------------------+
This does not hold. The problem is that while we are looping in state 0, we are threatened by the possibility of going to the state 1, where p does not hold.
The property infinitely often allows us to suspend our disbelief for the moment we will be in the state 1. The translation of the property from LTL to μ-calculus is non-trivial but well-known, 'lfp![X,gfp![Y, AX![X] || (p == 1 && AX![Y])]]'. Verifying with machine-check:
$ cargo run -- --property 'lfp![X,gfp![Y, AX![X] || (p == 1 && AX![Y])]]'
Finished `dev` profile [unoptimized + debuginfo] target(s) in 0.10s
warning: the following packages contain code that will be rejected by a future version of Rust: partitions v0.2.4
note: to see what the problems were, use the option `--future-incompat-report`, or run `cargo report future-incompatibilities --id 2`
Running `target\debug\hello-machine-check.exe --property "lfp![X,gfp![Y, AX![X] || (p == 1 && AX![Y])]]"`
[2025-10-28T22:30:45Z INFO machine_check] Starting verification.
[2025-10-28T22:30:45Z INFO machine_check::verify] Verifying the inherent property first.
[2025-10-28T22:30:45Z INFO machine_check::verify] The inherent property holds, proceeding to the given property.
[2025-10-28T22:30:45Z INFO machine_check::verify] Verifying the given property.
[2025-10-28T22:30:45Z INFO machine_check] Verification ended.
+------------------------------+
| Result: HOLDS |
+------------------------------+
| Refinements: 1 |
| Generated states: 8 |
| Final states: 3 |
| Generated transitions: 9 |
| Final transitions: 5 |
+------------------------------+
As such, p holds infinitely often but not eventually forever in this system.
⚠️ While μ-calculus properties must be by definition monotone, this is not enforced by the current version of machine-check in favour of richness of properties, and it is possible to e.g. force the verification into an infinite loop by verifying
lfp![X,!X], which will toggle the values of the fixed-point variable between zero and one infinitely. Monotonicity can be trivially ensured by only using AND and OR to manipulate the variable within its fixed point, without any negations or other applied functions/operators.
Underlying Research
Machine-check is based on a novel Input-based Three-valued Abstraction Refinement framework, which allows verification of properties in branching-time logics while using model-checking with abstraction refinement, which makes it possible to verify non-trivial systems.
The comprehensive overview of the research, with the contents of the folowing papers integrated, is given in Jan Onderka's dissertation thesis.
A preprint of the paper on the framework is available at arXiv:
- Onderka, J., Ratschan, S. Input-based three-valued abstraction refinement (preprint). arXiv:2408.12668 [cs.LO]. 2024.
Published papers on other techniques introduced for machine-check:
- Onderka, J. Formal verification of machine-code systems by translation of simulable descriptions. In Proceedings of the 13th Mediterranean Conference on Embedded Computing, MECO 2024. Budva, Montenegro, 2024. doi:10.1109/MECO62516.2024.10577942.
- Onderka, J., Ratschan, S. Fast three-valued abstract bit-vector arithmetic. In Finkbeiner, B., Wies, T., editors, Proceedings of the 23rd International Conference on Verification, Model Checking, and Abstract Interpretation, VMCAI 2022, pages 242–262. Springer Nature Switzerland, Cham, 2022. ISBN: 978-3-030-94583-1. doi:10.1007/978-3-030-94583-1_12.
The research might be too indigestible to most people (which is fine, since the point of the tool is that you shouldn't need to perfectly know what is happening underneath). For something simpler, consider this presentation:
- Onderka, J. Bridging verification of levels of digital systems using machine-check. 16th Alpine Verification Meeting (AVM'24).
Also see the blogposts about machine-check and the website of the main developer.
Version Migration
This page details the steps necessary to migrate the systems and properties to new versions of machine-check, starting from version 0.4.0. Note that this only covers systems and properties which successfully compile and execute without errors in the earlier version.
0.6.1 → 0.7.0
No changes necessary.
0.5.0 → 0.6.1
The properties now support μ-calculus, but the properties from version 0.5.0 can be used as-is without any changes. The systems must be modified as follows.
The machine_check::Input and machine_check::State traits are now blanket-implemented. Remove the following:
#![allow(unused)] fn main() { impl ::machine_check::Input for Input {} impl ::machine_check::State for State {} }
Parameters have been added to support parametric systems. For a non-parametric system (behaving as previously), add the following structure into the machine module:
#![allow(unused)] fn main() { #[derive(Clone, PartialEq, Eq, Hash, Debug)] pub struct Param {} }
Then, for the machine_check::Machine implementation, apply the changes as written in the comments:
#![allow(unused)] fn main() { impl ::machine_check::Machine for System { type Input = Input; type Param = Param; // <-- add this type State = State; // add the function argument '_param: &Param' as follows fn init(&self, input: &Input, _param: &Param) -> State { (...) } // add the function argument '_param: &Param' as follows fn next(&self, state: &State, input: &Input, _param: &Param) -> State { (...) } } }
Note that version 0.6.0 contained bugs that were fixed in version 0.6.1.
0.4.0 → 0.5.0
No changes necessary.